练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    11．不等式x2-x-2＜0的解集为（　　）
    A．{x|-2＜x＜1}B．{x|-1＜x＜2}C．{x|x＜-2或x＞1}D．{x|x＜-1或x＞2}

    分析 不等式x2-x-2＜0化为（x-2）（x+1）＜0，即可解出不等式x2-x-2＜0的解集．

    解答 解：不等式x2-x-2＜0化为（x-2）（x+1）＜0，解得-1＜x＜2．
    ∴不等式x2-x-2＜0的解集为{x|-1＜x＜2}．
    故选B．

    点评 本题考查了一元二次不等式的解法，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    7．已知圆A：x2+y2=1在伸缩变换$\left\{{\begin{array}{l}{x'=2x}\\{y'=3y}\end{array}}\right.$的作用下变成曲线C，则曲线C的方程为（　　）
    A．2x2+3y2=1B．4x2+9y2=1C．$\frac{{x}^{2}}{2}$+$\frac{{y}^{2}}{3}$=1D．$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{9}$=1

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

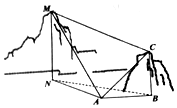    2．如图，为测量山高l，选择A和另一座山的山顶|PA|为测量观测点．从△ABC点测得MB=MC点的仰角∠MAN=75°，从A点测得C点的仰角∠CAB=30°以及∠MAC=75°，从C点测得∠MCA=60°．已知山高BC=80m，则山高MN=$120+40\sqrt{3}$（m）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．在下列向量组中，可以把向量$\overrightarrow{a}$=（3，-2）表示出来的是（　　）
    A．$\overrightarrow{{e}_{1}}$=（0，0），$\overrightarrow{{e}_{2}}$=（1，2）B．$\overrightarrow{{e}_{1}}$=（-1，2），$\overrightarrow{{e}_{2}}$=（5，-2）
    C．$\overrightarrow{{e}_{1}}$=（3，5），$\overrightarrow{{e}_{2}}$=（6，10）D．$\overrightarrow{{e}_{1}}$=（2，-3），$\overrightarrow{{e}_{2}}$=（-2，3）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．对于函数f（x）=$\left\{\begin{array}{l}{sinx，sinx≤cosx}\\{cosx，sinx＞cosx}\end{array}\right.$给出下列四个命题：
    ①该函数是以π为最小正周期的周期函数；
    ②当且仅当x=π+2kπ（k∈Z）时，该函数取得最小值-1；
    ③该函数的图象关于x=$\frac{5π}{4}$+2kπ（k∈Z）对称；
    ④当且仅当2kπ＜x＜$\frac{π}{2}$+2kπ（k∈Z）时，0＜f（x）≤$\frac{\sqrt{2}}{2}$
    其中正确命题的序号是③④．（请将所有正确命题的序号都填上）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．已知f（x）=excos x，则f′（$\frac{π}{2}$）的值为（　　）
    A．eπB．-eπC．-e${\;}^{\frac{π}{2}}$D．以上均不对

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知：向量$\vec a\;，\;\vec b\;，\;\vec c\;，\;\vec d$及实数x，y满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1，$\overrightarrow{c}$=$\overrightarrow{a}$+（x2-3）$\overrightarrow{b}$，$\overrightarrow{d}$=（-y）$\overrightarrow{a}$+x$\overrightarrow{b}$．若$\vec a⊥\vec b$，$\vec c⊥\vec d$且|$\overrightarrow{c}$|≤$\sqrt{10}$
    （1）求y=f（x）的函数解析式和定义域
    （2）若当$x∈（{1\;，\;\sqrt{6}}）$时，不等式$\frac{f（x）}{x}$≥mx-7恒成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．下列推理中属于归纳推理且结论正确的是（　　）
    A．由（1+1）2＞21，（2+1）2＞22，（3+1）2＞23，…，推断：对一切n∈N*，（n+1）2＞2n
    B．由f（x）=xcosx满足f（-x）=-f（x）对?x∈R都成立，推断：f（x）=xcosx为奇函数
    C．由圆x2+y2=r2的面积S=πr2，推断：椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的面积S=πab
    D．由an=2n-1，求出S1=12，S2=22，S3=32，…，推断：数列{an}的前n项和Sn=n2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．已知函数fn（x）=$\frac{1}{3}{x^3}-\frac{1}{2}（{n+1}）{x^2}+x（{n∈N*}）$，数列{an}满足an+1=f'n（an），a1=3．
    （1）是否存在n，使得fn（x）在x=1处取得极值，若存在，求n的值，若不存在，说明理由；
    （2）求a2，a3，a4的值，请猜想数列{an}的通项公式，并用数学归纳法证明．

    查看答案和解析>>

    同步练习册答案