
分析 (1)求出函数的导数,根据${f_n}^′(1)=0$,求出n的值,判断结论即可;
(2)猜想an=n+2,根据数学归纳法证明即可.
解答 解:(1)${f}_{n}^{′}$(x)=x2-(n+1)x+1,(n∈N*),
若fn(x)在x=1处取得极值,则${f_n}^′(1)=0$,得n=1,
此时${f_n}^′(x)={(x-1)^2}≥0$,所以fn(x)在R上单调递增,不存在极值.
所以不存在n,使得fn(x)在x=1处取得极值.
(2)由${f}_{n}^{′}$(x)=x2-(n+1)x+1,(n∈N*),
∴a1=3,又an+1=${{a}_{n}}^{2}$-(n+1)an+1,
∴a2=${{a}_{1}}^{2}$-2a1+1=4,
∴a3=${{a}_{2}}^{2}$-3a2+1=5,
∴a4=${{a}_{3}}^{2}$-4a3+1=6,
猜想an=n+2,
用数学归纳法证明,
①n=1时显然成立.
②假设当n=k(k∈N*)时,ak=k+2猜想成立,
则n=k(k∈N*)时,ak=k+2,
则当n=k+1(k∈N*)时,
ak+1=${{a}_{k}}^{2}$-(k+1)ak+1=(k+2)2-(k+1)(k+2)+1=k+3=(k+1)+2,
∴n=k+1时,猜想成立,
由①②可知对一切n∈N*,an=n+2成立.
点评 本题考查了函数的导数,极值问题,考查归纳猜想,考查数学归纳法的应用,是一道中档题.


科目:高中数学 来源: 题型:选择题
| A. | {x|-2<x<1} | B. | {x|-1<x<2} | C. | {x|x<-2或x>1} | D. | {x|x<-1或x>2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 甲 | 0 | 1 | 0 | 2 | 2 | 0 | 3 | 1 | 2 | 4 |
| 乙 | 2 | 3 | 1 | 1 | 0 | 2 | 1 | 1 | 0 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
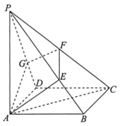 如图,在四棱锥P-ABCD中,底面ABCD为正方形,PA丄底面ABCD,PA=AC.过点A的平面与棱PB,PC,PD分别交于点E,F,G(E,F,G三点均不在棱的端点处).
如图,在四棱锥P-ABCD中,底面ABCD为正方形,PA丄底面ABCD,PA=AC.过点A的平面与棱PB,PC,PD分别交于点E,F,G(E,F,G三点均不在棱的端点处).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com