
分析 (1)由向量垂直的性质得y=x3-3x,再由|$\overrightarrow{c}$|≤$\sqrt{10}$,得x4-6x2≤0,由此能求出y=f(x)的函数解析式和定义域.
(2)不等式即为x2-3≥mx-7,即m$≤x+\frac{4}{x}$在x∈(1,$\sqrt{6}$)上恒成立,由此能求出实数m的取值范围.
解答 解:(1)∵向量$\vec a\;,\;\vec b\;,\;\vec c\;,\;\vec d$及实数x,y满足
$\overrightarrow{c}$=$\overrightarrow{a}$+(x2-3)$\overrightarrow{b}$,$\overrightarrow{d}$=(-y)$\overrightarrow{a}$+x$\overrightarrow{b}$.$\vec a⊥\vec b$,$\vec c⊥\vec d$,
∴$\overrightarrow{a}•\overrightarrow{b}$=0,$\overrightarrow{c}•\overrightarrow{d}=0$,
∴-y${\overrightarrow{a}}^{2}$+x(x2-3)${\overrightarrow{b}}^{2}$=0,
∵|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1,∴y=x3-3x,
∵|$\overrightarrow{c}$|≤$\sqrt{10}$,∴${\overrightarrow{a}}^{2}+({x}^{2}-3){\overrightarrow{b}}^{2}$≤10,
∴x4-6x2≤0,∴-$\sqrt{6}≤x≤\sqrt{6}$,
∴f(x)=x3-3x,x∈[-$\sqrt{6},\sqrt{6}$].
(2)不等式即为x2-3≥mx-7,
即m$≤x+\frac{4}{x}$在x∈(1,$\sqrt{6}$)上恒成立,
故(x+$\frac{4}{x}$)min=4,∴m≤4,
∴实数m的取值范围是(-∞,4].
点评 本题考查平面向量运算、向量垂直的性质等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
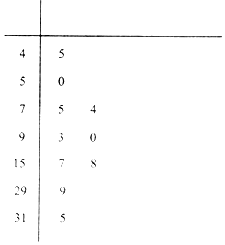 近年来,空气质量成为人们越来越关注的话题,空气质量指数(AirQualityIndex,简称AQI)是定量描述空气质量状况的指数,空气质量按照AQI大小分为六级,0~50为优;51~100为良;101~150为轻度污染;151~200为中度污染;201~300为重度污染;大于300为严重污染.环保部门记录了2017年某月哈尔滨市10天的AQI的茎叶图如下:
近年来,空气质量成为人们越来越关注的话题,空气质量指数(AirQualityIndex,简称AQI)是定量描述空气质量状况的指数,空气质量按照AQI大小分为六级,0~50为优;51~100为良;101~150为轻度污染;151~200为中度污染;201~300为重度污染;大于300为严重污染.环保部门记录了2017年某月哈尔滨市10天的AQI的茎叶图如下:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {$\frac{5π}{4}$} | B. | {$\frac{π}{4}$} | C. | {2kπ+$\frac{π}{4}$}(k∈Z) | D. | {kπ+$\frac{π}{4}$}(k∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-2<x<1} | B. | {x|-1<x<2} | C. | {x|x<-2或x>1} | D. | {x|x<-1或x>2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a,b中至少有一个为0 | B. | a,b中至少有一个不为0 | ||
| C. | a,b全为0 | D. | a,b中只有一个不为0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,-1) | B. | (-3,1) | C. | (-3,-1) | D. | (3,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 甲 | 0 | 1 | 0 | 2 | 2 | 0 | 3 | 1 | 2 | 4 |
| 乙 | 2 | 3 | 1 | 1 | 0 | 2 | 1 | 1 | 0 | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com