
成都市为“市中学生知识竞赛”进行选拔性测试,且规定:成绩大于或等于90分的有参赛资格,90分以下(不包括90分)的则被淘汰。若现有500人参加测试,学生成绩的频率分布直方图如下: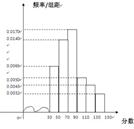
(I)求获得参赛资格的人数;
(II)根据频率直方图,估算这500名学生测试的平均成绩;
(III)若知识竞赛分初赛和复赛,在初赛中每人最多有5次选题答题的机会,累计答对3题或答错3题即终止,答对3题者方可参加复赛,已知参赛者甲答对每一个问题的概率都相同,并且相互之间没有影响,已知他连续两次答错的概率为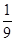 ,求甲在初赛中答题个数的分布列及数学期望.
,求甲在初赛中答题个数的分布列及数学期望.
(I) 125;(II)78.48;(III) 分布列为:
数学期望为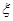
3 4 5 
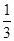
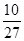
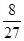
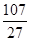 .
.
解析试题分析:(I)将频率分布直方图中90~150的小矩形的面积相加,便得获得参赛资格的人数的频率.频率乘以测试总人数500,便得获得参赛资格的人数.
(II)在频率分布直方图中,平均值等于每小组的频率乘以每小组中点的值的和.
(III)已知连续两次答错的概率为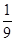 ,由此可得答对每一道题的概率.注意,答题的个数
,由此可得答对每一道题的概率.注意,答题的个数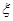 包括答对的和答错的.显然答题的个数
包括答对的和答错的.显然答题的个数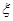 可取3、4、5. “
可取3、4、5. “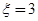 ”表示连续答对3个或连续答错3个;“
”表示连续答对3个或连续答错3个;“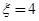 ”表示前3题中恰好答对2个且第4 个题答对或前3题中恰好答错2个且第4 个题答错;“
”表示前3题中恰好答对2个且第4 个题答对或前3题中恰好答错2个且第4 个题答错;“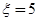 ”表示前4个题恰好答对2个.根据独立事件的概率公式便可得
”表示前4个题恰好答对2个.根据独立事件的概率公式便可得 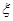 的分布列,由随机变量的数学期望公式可求得
的分布列,由随机变量的数学期望公式可求得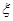 的期望.
的期望.
试题解析:(I)获得参赛资格的人数 2分
2分
(II)平均成绩:
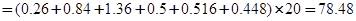 5分
5分
(III)设甲答对每一道题的概率为.P
则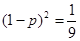
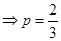
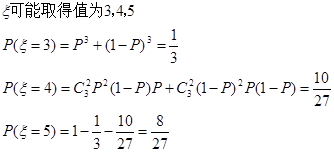
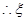 的分布列为
的分布列为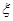
3 4 5 
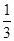
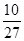
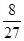
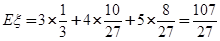 12分
12分
考点:1、频率分布直方图及样本数据的平均数;2、随机变量的分布列及期望.


科目:高中数学 来源: 题型:解答题
从某年级学生中,随机抽取50人,其体重(单位:千克)的频数分布表如下:
| 分组(体重) | 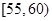 | 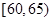 | 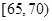 | 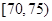 |
| 频数(人) | 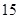 | 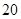 | 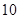 | 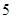 |
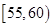 的频率;
的频率;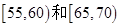 中共有几人?
中共有几人?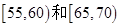 的人中,任取2人,求体重在
的人中,任取2人,求体重在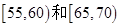 中各有1人的概率.
中各有1人的概率.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某中学对高三年级进行身高统计,测量随机抽取的20名学生的身高,其频率分布直方图如下(单位:cm)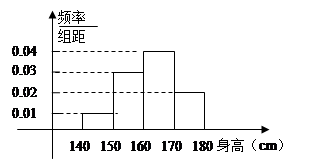
(1)根据频率分布直方图,求出这20名学生身高中位数的估计值和平均数的估计值.
(2)在身高为140—160的学生中任选2个,求至少有一人的身高在150—160之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某中学对高三年级进行身高统计,测量随机抽取的20名学生的身高,其频率分布直方图如下(单位:cm)
(1)根据频率分布直方图,求出这20名学生身高中位数的估计值和平均数的估计值;
(2)在身高为140—160的学生中任选2个,求至少有一人的身高在150—160之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某学校100名学生期中考试语文成绩的频率分布直方图如下右图所示,其中成绩分组区间是: ,
,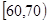 ,
, ,
,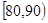 ,
, 。
。
求图中a的值;
根据频率分布直方图,估计这100名学生语文成绩的平均分;
若这100名学生语文成绩某些分数段的人数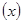 与数学成绩相应分数段的人数
与数学成绩相应分数段的人数
之比如下表所示,求数学成绩在 之外的人数。
之外的人数。
| 分数段 |  | 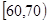 |  | 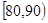 |
x :y :y | 1:1 | 2:1 | 3:4 | 4:5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
由世界自然基金会发起的“地球1小时”活动,已发展成为最有影响力的环保活动之一,今年的参与人数再创新高,然而也有部分公众对该活动的实际效果与负面影响提出了疑问,对此,某新闻媒体进行了网上调查,所有参与调查的人中,持“支持”、“保留”和“不支持”态度的人数如下表所示:
| | 支持 | 保留 | 不支持 |
| 20岁以下 | 800 | 450 | 200 |
| 20岁以上(含20岁) | 100 | 150 | 300 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某地区因干旱缺水,政府向市民宣传节约用水,并进行广泛动员 三个月后,统计部门在一个小区随机抽取了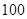 户家庭,分别调查了他们在政府动员前后三个月的月平均用水量(单位:吨),将所得数据分组,画出频率分布直方图(如图所示)
户家庭,分别调查了他们在政府动员前后三个月的月平均用水量(单位:吨),将所得数据分组,画出频率分布直方图(如图所示)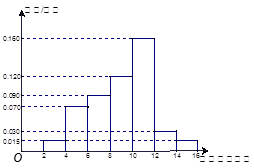
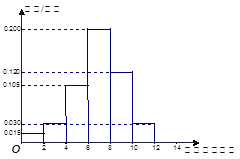
动员前 动员后
(Ⅰ)已知该小区共有居民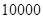 户,在政府进行节水动员前平均每月用水量是
户,在政府进行节水动员前平均每月用水量是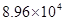 吨,请估计该小区在政府动员后比动员前平均每月节约用水多少吨;
吨,请估计该小区在政府动员后比动员前平均每月节约用水多少吨;
(Ⅱ)为了解动员前后市民的节水情况,媒体计划在上述家庭中,从政府动员前月均用水量在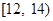 内的家庭中选出
内的家庭中选出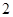 户作为采访对象,其中甲、乙两家在备选之列,求恰好选中他们两家作为采访对象的概率
户作为采访对象,其中甲、乙两家在备选之列,求恰好选中他们两家作为采访对象的概率
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某高校在2011年自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示.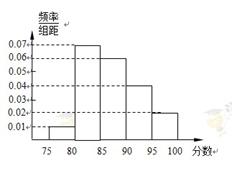
(1)分别求第3,4,5组的频率;
(2)若该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试.
① 已知学生甲和学生乙的成绩均在第三组,求学生甲和学生乙同时进入第二轮面试的概率;
② 学校决定在这6名学生中随机抽取2名学生接受考官的面试,设第4组中有X名学生被考官面试,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
以下是某地搜集到的新房屋的销售价格y和房屋的面积x的数据:
| 房屋面积(m2) | 115 | 110 | 80 | 135 | 105 |
| 销售价格(万元) | 24.8 | 21.6 | 18.4 | 29.2 | 22 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com