
【题目】过直线y=﹣1上的动点A(a,﹣1)作抛物线y=x2的两切线AP,AQ,P,Q为切点.
(1)若切线AP,AQ的斜率分别为k1,k2,求证:k1k2为定值.
(2)求证:直线PQ过定点.
【答案】(1)证明见解析(2)证明见解析
【解析】
(1)设过A作抛物线y=x2的切线的斜率为k,用选定系数法给出切线的方程,与抛物线方程联立消元得到关于x的一元二次方程,此一元二次方程仅有一根,故其判别式为0,得到关于k的一元二次方程,k1,k2必为其二根,由根系关系可求得两根之积为定值,即k1k2为定值;
(2)设P(x1,y1),Q(x2,y2),用其坐标表示出两个切线的方程,因为A点是两切线的交点将其坐标代入两切线方程,观察发现P(x1,y1),Q(x2,y2)的坐标都适合方程2ax﹣y+1=0上,因为两点确定一条直线,故可得过这两点的直线方程必为2ax﹣y+1=0,该线过定点(0,1)故证得.
(1)设过A作抛物线y=x2的切线的斜率为k,
则切线的方程为y+1=k(x﹣a),
与方程y=x2联立,消去y,得x2﹣kx+ak+1=0.
因为直线与抛物线相切,所以△=k2﹣4(ak+1)=0,
即k2﹣4ak﹣4=0.由题意知,此方程两根为k1,k2,
∴k1k2=﹣4(定值);
(2)设P(x1,y1),Q(x2,y2),由y=x2,得y′=2x.
所以在P点处的切线斜率为:![]() ,
,
因此,切线方程为:y﹣y1=2x1(x﹣x1).
由y1=x12,化简可得,2x1x﹣y﹣y1=0.
同理,得在点Q处的切线方程为2x2x﹣y﹣y2=0.
因为两切线的交点为A(a,﹣1),故2x1a﹣y1+1=0,2x2a﹣y2+1=0.
∴P,Q两点在直线2ax﹣y+1=0上,即直线PQ的方程为:2ax﹣y+1=0.
当x=0时,y=1,所以直线PQ经过定点(0,1).


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知圆![]() 经过抛物线
经过抛物线![]() 的焦点
的焦点![]() ,且与抛物线
,且与抛物线![]() 的准线
的准线![]() 相切.
相切.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)设经过点![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() 两点,点
两点,点![]() 关于
关于![]() 轴的对称点为点
轴的对称点为点![]() ,若
,若![]() 的面积为6,求直线
的面积为6,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某校打算在长为1千米的主干道![]() 一侧的一片区域内临时搭建一个强基计划高校咨询和宣传台,该区域由直角三角形区域
一侧的一片区域内临时搭建一个强基计划高校咨询和宣传台,该区域由直角三角形区域![]() (
(![]() 为直角)和以
为直角)和以![]() 为直径的半圆形区域组成,点
为直径的半圆形区域组成,点![]() (异于
(异于![]() ,
,![]() )为半圆弧上一点,点
)为半圆弧上一点,点![]() 在线段
在线段![]() 上,且满足
上,且满足![]() .已知
.已知![]() ,设
,设![]() ,且
,且![]() .初步设想把咨询台安排在线段
.初步设想把咨询台安排在线段![]() ,
,![]() 上,把宣传海报悬挂在弧
上,把宣传海报悬挂在弧![]() 和线段
和线段![]() 上.
上.
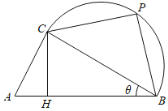
(1)若为了让学生获得更多的咨询机会,让更多的省内高校参展,打算让![]() 最大,求该最大值;
最大,求该最大值;
(2)若为了让学生了解更多的省外高校,贴出更多高校的海报,打算让弧![]() 和线段
和线段![]() 的长度之和最大,求此时的
的长度之和最大,求此时的![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() ,
,![]() 分别是其左、右焦点,且过点
分别是其左、右焦点,且过点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若在直线![]() 上任取一点
上任取一点![]() ,从点
,从点![]() 向
向![]() 的外接圆引一条切线,切点为
的外接圆引一条切线,切点为![]() .问是否存在点
.问是否存在点![]() ,恒有
,恒有![]() ?请说明理由.
?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥O﹣ABCD的底面是边长为1的菱形,OA=2,∠ABC=60°,OA⊥平面ABCD,M、N分别是OA、BC的中点.
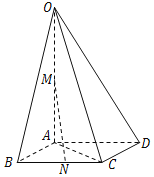
(1)求证:直线MN∥平面OCD;
(2)求点M到平面OCD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《高中数学课程标准》(2017版)规定了数学直观想象学科的六大核心素养,为了比较甲、乙两名高二学生的数学核心素养水平,现以六大素养为指标对二人进行了测验,根据测验结果绘制了雷达图(如图,每项指标值满分为5分,分值高者为优),则下面叙述正确的是(注:雷达图![]() ,又可称为戴布拉图、蜘蛛网图
,又可称为戴布拉图、蜘蛛网图![]() ,可用于对研究对象的多维分析)( )
,可用于对研究对象的多维分析)( )
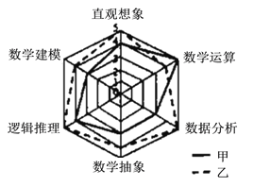
A.甲的直观想象素养高于乙
B.甲的数学建模素养优于数据分析素养
C.乙的数学建模素养与数学运算素养一样
D.乙的六大素养整体水平低于甲
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com