已知函数f(x)=lnx,g(x)=a(x2-x)(a≠0,a∈R),h(x)=f(x)-g(x)
(I)若a=1,求函数h(x)的极值;
(II )若函数y=h (x)在(1,+∞)上单调递增,求实数a的取值范围;
(III)在函数:y=f(x)的图象上是否存在不同的两点A(x1,y1),B(x2,y2),使线段AB的中点的横坐标x0与直线AB的斜率k之间满足k=f′(x0)?若存在,求出x0;若不存在,请说明理由.
解:(Ⅰ)由f(x)=lnx,g(x)=a(x
2-x)(a≠0,a∈R),
得:h(x)=f(x)-g(x)=lnx-ax
2+ax,
当a=1时,h(x)=lnx-x
2+x.

=

.
∵函数h(x)的定义域为(0,+∞),且当x∈(0,1)时,h
′(x)>0,h(x)在(0,1)上单调递增,
当x∈(1,+∞)时,h
′(x)<0,h(x)在(1,+∞)上单调递减,
∴h(x)有极大值h(1)=0,无极小值;
(Ⅱ)h(x)=f(x)-g(x)=lnx-ax
2+ax,
则
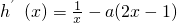
.
∵函数y=h(x)在(1,+∞)上单调递增,则
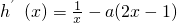
≥0对x>1恒成立.
即
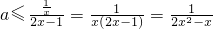
对x>1恒成立.
∵x>1时,2x
2-x>1,∴
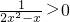
,又a≠0,∴a<0.
则a的取值范围是(-∞,0).
(Ⅲ)假设存在,不妨设0<x
1<x
2,
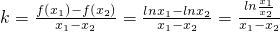
,
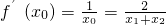
,
由k=f
′(x
0)?
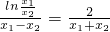
,
∴
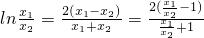
.
令t=

,u(t)=
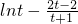
(0<t<1),则
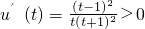
,
∴u(t)在(0,1)上单调递增,∴u(t)<u(1)=0,
∴
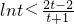
,即
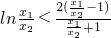
.
故k≠f
′(x
0).
所以不存在符合题意的两点.
分析:(Ⅰ)写出h(x),把a=1代入后求导函数,求出导函数在定义域内的零点,然后判断导函数在不同区间段内的符号,从而得到原函数的单调性,最后得到函数h(x)的极值情况;
(Ⅱ)根据函数y=h (x)在(1,+∞)上单调递增,则其导函数在(1,+∞)内大于0恒成立,分离变量后可求不等式一侧所对应的函数的值域,从而求出a的取值范围;
(Ⅲ)利用反证法思想,假设两点存在,由线段AB的中点的横坐标x
0与直线AB的斜率k之间满足k=f′(x
0),利用两点求斜率得到k,把x
0也用两点的横坐标表示,整理后得到∴
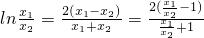
,令t=

,引入函数u(t)=
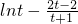
(0<t<1),通过求函数的导函数判断函数单调性得到即
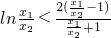
,从而得出矛盾,说明假设错误.
点评:本题考查了函数的单调性与导数之间的关系,考查了利用导数分析函数的极值,考查了利用分离变量法求参数的取值范围,训练了反证法解题的基本思想,(Ⅲ)中的转化、变形及构造函数推出矛盾结论是该题的难点,此题属难度较大的题目.

 =
= .
.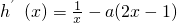 .
.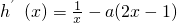 ≥0对x>1恒成立.
≥0对x>1恒成立.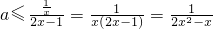 对x>1恒成立.
对x>1恒成立.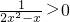 ,又a≠0,∴a<0.
,又a≠0,∴a<0.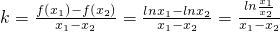 ,
,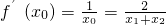 ,
,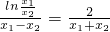 ,
,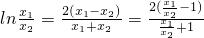 .
. ,u(t)=
,u(t)=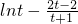 (0<t<1),则
(0<t<1),则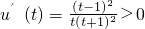 ,
,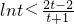 ,即
,即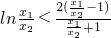 .
.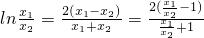 ,令t=
,令t= ,引入函数u(t)=
,引入函数u(t)=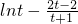 (0<t<1),通过求函数的导函数判断函数单调性得到即
(0<t<1),通过求函数的导函数判断函数单调性得到即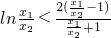 ,从而得出矛盾,说明假设错误.
,从而得出矛盾,说明假设错误.
