
(本题14分)已知直线![]() :y=kx+1与双曲线C:2x2-y2=1的右支交于不同的两点A、B。(1)求实数k的取值范围;(2)是否存在实数k,使得以线段AB为直径的圆经过双曲线C的右焦点F?若荐在,求出k的值。若不存在,说明理由。
:y=kx+1与双曲线C:2x2-y2=1的右支交于不同的两点A、B。(1)求实数k的取值范围;(2)是否存在实数k,使得以线段AB为直径的圆经过双曲线C的右焦点F?若荐在,求出k的值。若不存在,说明理由。
(Ⅰ) -2<k<-![]() (Ⅱ)
(Ⅱ) ![]()
(1)将直线![]() 的方程y=kx+1代入双曲线C的方程2x2-y2=1后,整理得(k2-2)x2+2kx+2=0, 依题意,直线
的方程y=kx+1代入双曲线C的方程2x2-y2=1后,整理得(k2-2)x2+2kx+2=0, 依题意,直线![]() 与双曲线C的右支交于不同两点,则
与双曲线C的右支交于不同两点,则
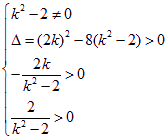 ,解得k的取值范围为-2<k<-
,解得k的取值范围为-2<k<-![]() .
.
(2)设A、B两点的坐标分别为(x1,y1),(x2,y2),则由①得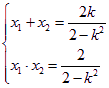 ………①,
………①,
假设存在实数k,使得以线段AB为直径的圆经过双曲线C的右焦点F(c,0),则由FA⊥FB得:(x1-c)(x2-c)+y1y2=0,即(x1-c)(x2-c)+(kx1+1)(kx2+1)=0,整理得:
(k2+1)x1 x2+(k-c)(x1 +x2)+c2+1=0…………………②,
把①式及c=![]() 代入②式化简得:
代入②式化简得:![]() ,解得
,解得![]() 或
或
![]() (舍去)可知
(舍去)可知![]() 使得以线段AB为直径的圆经过双曲线C的右焦点。
使得以线段AB为直径的圆经过双曲线C的右焦点。


 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:
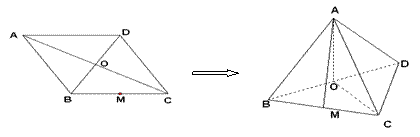
(本题满分14分)已知菱形![]() 的边长为2,对角线
的边长为2,对角线![]() 与
与![]() 交于点
交于点![]() ,且
,且![]() ,
,![]() 为
为![]() 的中点.将此菱形沿对角线
的中点.将此菱形沿对角线![]() 折成直二面角
折成直二面角![]() .
.
(I)求证:![]() ;
;
(II)求直线![]() 与面
与面![]() 所成角的余弦值大小.
所成角的余弦值大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分14分)
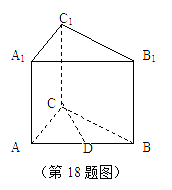 已知直三棱柱
已知直三棱柱![]() D是AB的中点.
D是AB的中点.
(1)求证:CD⊥平面ABB1A1;
(2)求二面角D—A1C—A的正切值;
(3)求点C1到平面A1CD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分14分)
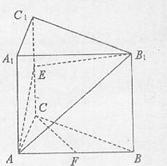
如图,已知直三棱柱ABC—A1B1C1,![]() ,E是棱CC1上动点,F是AB中点,
,E是棱CC1上动点,F是AB中点,![]()
(1)求证:![]() ;
;
(2)当E是棱CC1中点时,求证:CF//平面AEB1;
(3)在棱CC1上是否存在点E,使得二面角A—EB1—B的大小是45°,若存在,求CE的长,若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源:2011届广东省华南师大附中高三综合测试数学理卷 题型:解答题
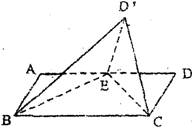
(本题满分14分) 已知矩形ABCD,AD=2AB=2,点E是AD的中点,将△DEC
沿CE折起到△D’EC的位置,使二面角D'-EC -B是直二面角。
(Ⅰ) 证明:BE⊥CD’;
(Ⅱ) 求二面角D'-BC -E的余弦值,
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省高三综合测试数学理卷 题型:解答题
(本题满分14分) 已知矩形ABCD,AD=2AB=2,点E是AD的中点,将△DEC
沿CE折起到△D’EC的位置,使二面角D'-EC -B是直二面角。
(Ⅰ) 证明:BE⊥CD’;
(Ⅱ) 求二面角D'-BC -E的余弦值,
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com