
| A. | 2 | B. | $\sqrt{2}$ | C. | 3 | D. | $\sqrt{2}+1$ |
分析 由条件即可取$\overrightarrow{a}=(1,0),\overrightarrow{b}=(0,1),\overrightarrow{c}=(x,y)$,进而可求出$\overrightarrow{c}-\overrightarrow{a}-\overrightarrow{b}$的坐标,从而可得到(x-1)2+(y-1)2=1,这样即可设x=cosα+1,y=sinα+1,从而求出$|\overrightarrow{c}|=\sqrt{3+2\sqrt{2}sin(α+\frac{π}{4})}$,这样即可求出$|\overrightarrow{c}|$的最大值.
解答 解:根据条件,取$\overrightarrow{a}=(1,0),\overrightarrow{b}=(0,1),\overrightarrow{c}=(x,y)$;
∴$\overrightarrow{c}-\overrightarrow{a}-\overrightarrow{b}=(x-1,y-1)$;
∵$|\overrightarrow{c}-\overrightarrow{a}-\overrightarrow{b}|=1$;
∴(x-1)2+(y-1)2=1;
设$\left\{\begin{array}{l}{x=cosα+1}\\{y=sinα+1}\end{array}\right.$;
∴$|\overrightarrow{c}|=\sqrt{{x}^{2}+{y}^{2}}=\sqrt{(cosα+1)^{2}+(sinα+1)^{2}}$=$\sqrt{3+2(sinα+cosα)}$=$\sqrt{3+2\sqrt{2}sin(α+\frac{π}{4})}$;
∴$sin(α+\frac{π}{4})=1$时,$|\overrightarrow{c}|$取最大值$\sqrt{3+2\sqrt{2}}=\sqrt{2}+1$.
故选:D.
点评 考查引入坐标解决向量问题的方法,向量坐标的减法运算,根据向量坐标求向量长度的方法,以及两角和的正弦公式.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 板材类型 | A | B | C |
| 甲型石板(块) | 1 | 2 | 4 |
| 乙型石板(块) | 2 | 1 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
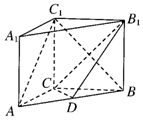 如图所示,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.
如图所示,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{3}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{{\sqrt{5}}}{5}$ | D. | $-\frac{{2\sqrt{5}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | $\frac{3}{2}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com