练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
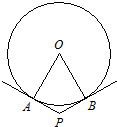
    （2008•普陀区一模）在120°的二面角内放一个半径为6的球，使球与两个半平面各只有一个公共点（其过球心且垂直于二面角的棱的直截面如图所示），则这两个公共点AB之间的球面距离为
    2π
    2π
    ．
    分析：由题意可得，APB=120°，根据切线的性质可得，OA⊥AP，OB⊥PB，从而可得∠AOB=60°，根据AB球面距离公式l=α•r可求
    解答：解：由题意可得，APB=120°
    连接OA，OB，则根据切线的性质可得，OA⊥AP，OB⊥PB
    ∴∠AOB=60°
    △AOB为等边三角形
    AB之间的球面距离l=α•r=
    π
    3
    ×6=2π
    故答案为：2π
    点评：本题主要考查了二面角的平面角的应用，球面距离的求解，属于基础试题
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （2008•普陀区一模）一个圆柱形容器的轴截面尺寸如右图所示，容器内有一个实心的球，球的直径恰等于圆柱的高．现用水将该容器注满，然后取出该球（假设球的密度大于水且操作过程中水量损失不计），则球取出后，容器中水面的高度为
    25
    3
    25
    3
    cm．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2008•普陀区一模）抛物线y2=-8x的焦点坐标为
    （-2，0）
    （-2，0）
    ；准线方程为
    x=2
    x=2
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2008•普陀区一模）对任意的实数α、β，下列等式恒成立的是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2008•普陀区一模）如图，在直三棱柱ABC-A1B1C1中，CC1=AC=BC，∠ACB=90°，P是AA1的中点，Q是AB的中点．
    （1）求异面直线PQ与B1C所成角的大小；
    （2）若直三棱柱ABC-A1B1C1的体积为
    12
    ，求四棱锥C-BAPB1的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2008•普陀区一模）已知函数f(x)=
    2x
    3•2x+1
    ，则f-1(
    1
    4
    )    =
    0
    0
    ．

    查看答案和解析>>

    同步练习册答案