
分析 (Ⅰ)由曲线C1的参数方程知:曲线C1是过点(-1,3)的直线,相加消去参数t可得:曲线C1的普通方程.曲线C2的极坐标方程为ρ=2$\sqrt{2}$sin(θ+$\frac{π}{4}$),展开可得ρ2=2$\sqrt{2}×\frac{\sqrt{2}}{2}$ρ(sinθ+cosθ),利用互化公式可得曲线C2的直角坐标方程.
(Ⅱ)由判断知:P在直线C1上,将$\left\{\begin{array}{l}x=-1-\frac{{\sqrt{2}}}{2}t\\ y=3+\frac{{\sqrt{2}}}{2}t\end{array}\right.$代入曲线C2的方程得:${t^2}+4\sqrt{2}t+6=0$,利用|PB|•|PD|=|t1|•|t2|=|t1t2|即可得出.
解答 解:(Ⅰ)由曲线C1的参数方程知:曲线C1是过点(-1,3)的直线,
相加消去参数t可得:曲线C1的普通方程为x+y-2=0.
曲线C2的极坐标方程为ρ=2$\sqrt{2}$sin(θ+$\frac{π}{4}$),
展开可得ρ2=2$\sqrt{2}×\frac{\sqrt{2}}{2}$ρ(sinθ+cosθ),
利用互化公式可得:曲线C2的直角坐标方程为x2+y2-2x-2y=0.
(Ⅱ)由判断知:P在直线C1上,
将$\left\{\begin{array}{l}x=-1-\frac{{\sqrt{2}}}{2}t\\ y=3+\frac{{\sqrt{2}}}{2}t\end{array}\right.$代入方程x2+y2-2x-2y=0得:${t^2}+4\sqrt{2}t+6=0$,
设点B,D对应的参数分别为t1,t2,
则|PB|=|t1|,|PD|=|t2|,而t1t2=6,
∴|PB|•|PD|=|t1|•|t2|=|t1t2|=6.
点评 本题考查了极坐标方程与直角坐标方程互化、参数方程的应用、直线与相交相交转化为一元二次方程的根与系数的关系,考查了推理能力与计算能力,属于中档题.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
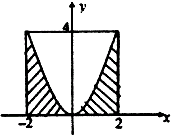 如图,设D是图中边长为4的正方形区域,E是D内由幂函数y=m•xa图象下方阴影部分的点构成的区域,在D内随机取一点,则该点在E中的概率为( )
如图,设D是图中边长为4的正方形区域,E是D内由幂函数y=m•xa图象下方阴影部分的点构成的区域,在D内随机取一点,则该点在E中的概率为( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在如图所示的几何体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE,M是AB的中点.
在如图所示的几何体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE,M是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com