
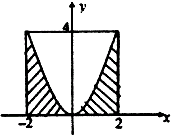
 如图,设D是图中边长为4的正方形区域,E是D内由幂函数y=m•xa图象下方阴影部分的点构成的区域,在D内随机取一点,则该点在E中的概率为( )
如图,设D是图中边长为4的正方形区域,E是D内由幂函数y=m•xa图象下方阴影部分的点构成的区域,在D内随机取一点,则该点在E中的概率为( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
分析 根据几何概型概率公式结合定积分求面积的方法易求解.
解答 解:由题意,m=1,(2,4)代入y=m•xa,可得a=2,
∴y=x2,
区域E的面积为:S1=${∫}_{-2}^{2}{x}^{2}dx$=$\frac{1}{3}{x}^{3}{|}_{-2}^{2}$=$\frac{16}{3}$
∴“该点在E中的概率”事件对应的区域面积为$\frac{16}{3}$,
则质点落在区域M内的概率是$\frac{\frac{16}{3}}{{4}^{2}}$=$\frac{1}{3}$.
故选C.
点评 本题综合考查了二次函数的图象,几何概型,及定积分在求面积中的应用,考查计算能力与转化思想.属于基础题.


 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源: 题型:选择题
| A. | 某事件发生的概率为P(A)=1.1 | |
| B. | 不可能事件的概率为0,必然事件的概率为1 | |
| C. | 小概率事件就是不可能发生的事件,大概率事件就是必然要发生的事件 | |
| D. | 某事件发生的概率是随着试验次数的变化而变化的 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{1}{16}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{27}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (9,49) | B. | (13,49] | C. | (13,45) | D. | (13,49) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 过定点(0,1) | B. | 过定点(0,2) | C. | 过定点(a,1) | D. | 过定点(a,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com