
分析 (1)把已知等式变形,可得$sinα+cosα=\frac{{\sqrt{2}}}{3}$,两边平方后求得sinαcosα的值,结合已知可得sinα>0>cosα,从而得$sinα-cosα=\sqrt{{{(sinα-cosα)}^2}}=\frac{4}{3}$.
联立$\left\{\begin{array}{l}sinα-cosα=\frac{4}{3}\\ sinα+cosα=\frac{{\sqrt{2}}}{3}\end{array}\right.$,求得sinα,cosα的值,则tanα可求;
(2)利用诱导公式变形,然后化为完全平方式,开方得答案.
解答 解:(1)由$cos({\frac{π}{2}+α})+cos({π+α})=-\frac{{\sqrt{2}}}{3}$得:$sinα+cosα=\frac{{\sqrt{2}}}{3}$;
两边平方得:$2sinαcosα=-\frac{7}{9}$,
∵$\frac{π}{2}<α<π$,∴sinα>0>cosα,
故$sinα-cosα=\sqrt{{{(sinα-cosα)}^2}}=\frac{4}{3}$.
∵$\left\{\begin{array}{l}sinα-cosα=\frac{4}{3}\\ sinα+cosα=\frac{{\sqrt{2}}}{3}\end{array}\right.$;
∴$\left\{\begin{array}{l}sinα=\frac{{\sqrt{2}+4}}{6}\\ cosα=\frac{{\sqrt{2}-4}}{6}\end{array}\right.$,则$tanα=-\frac{{9+4\sqrt{2}}}{7}$;
(2)$\sqrt{1-2sin({π+α})cos({π+α})}$=$\sqrt{1-2sin({π+2})cos({π+2})}$=|sin2-cos2|,
∵sin2>0,cos2<0,
∴$\sqrt{1-2sin({π+α})cos({π+α})}$=sin2-cos2.
点评 本题考查三角函数中的恒等变换应用,考查同角三角函数的基本关系式及诱导公式的应用,属中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | ex | B. | ex+$\frac{1}{3}$ | C. | $\frac{1}{3}$ | D. | ex-$\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
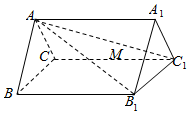 如图所示,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,点M是棱CC1的中点.
如图所示,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,点M是棱CC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 5 | ||
| 女生 | 10 | ||
| 合计 | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 当n=2时,f(2)=$\frac{1}{2}$+$\frac{1}{3}$;f(k+1)比f(k)多了1项 | |
| B. | 当n=2时,f(2)=$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$;f(k+1)比f(k)多了2k+1项 | |
| C. | 当n=2时,f(2)=$\frac{1}{2}$+$\frac{1}{3}$;f(k+1)比f(k)多了k项 | |
| D. | 当n=2时,f(2)=$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$;f(k+1)比f(k)多了2k项 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com