
6个人坐在一排10个座位上,则(用数字表示).
(1)空位不相邻的坐法有多少种?
(2)4个空位只有3个相邻的坐法有多少种?
(3)4个空位至多有2个相邻的坐法有多少种?
(1)25200;(2)30240;(3)115920.
【解析】
试题分析:(1)根据空位不相邻,6人先坐在6个座位上并排好顺序,后将4个空位采用插空法插入即可达到要求;(2)6人先坐在6个座位上并排好顺序,先将3个空位捆绑当作一个空位,再将生产的“两个”空位采用插空法插入即可;(3)法一:采用间接法,将所有可能的坐法 ,减去四个空位相邻的坐法
,减去四个空位相邻的坐法 ,再减去只有3个空位相邻的坐法
,再减去只有3个空位相邻的坐法 即可;法二:直接法,分成三类,第一类是空位都不相邻的坐法,第二类是4个空位中只有两个空位相邻的,另两个不相邻,第三类是4个空位中,两个空位相邻,另两个空位也相邻,然后将这三种情况的坐法相加即可.
即可;法二:直接法,分成三类,第一类是空位都不相邻的坐法,第二类是4个空位中只有两个空位相邻的,另两个不相邻,第三类是4个空位中,两个空位相邻,另两个空位也相邻,然后将这三种情况的坐法相加即可.
(1)第一步:6人先坐在6个座位上并排好顺序有 种,第二步:将4个空位插入有:
种,第二步:将4个空位插入有: ,所以空位不相邻的坐法共有:
,所以空位不相邻的坐法共有: 种;
种;
(2)第一步:6人先坐在6个座位上并排好顺序有 ,第二步:先将3个空位捆绑当作一个空位,再将生产的“两个”空位采用插空法插入有:
,第二步:先将3个空位捆绑当作一个空位,再将生产的“两个”空位采用插空法插入有: 种,所以4个空位只有3个相邻的坐法有:
种,所以4个空位只有3个相邻的坐法有: 种;
种;
(3)法一:采用间接法,所有可能的坐法有 种,四个空位相邻的坐法有
种,四个空位相邻的坐法有 ,只有3个空位相邻的坐法有
,只有3个空位相邻的坐法有 种,所以4个空位至多有2个相邻的坐法有
种,所以4个空位至多有2个相邻的坐法有
法二:直接法,分成三类:
第一类是空位都不相邻的坐法有 ;
;
第二类是4个空位中只有两个空位相邻的,另两个不相邻的坐法有: 种;
种;
第三类是4个空位中,两个空位相邻,另两个空位也相邻的坐法有: 种;
种;
所以4个空位至多有2个相邻的坐法有 种.
种.
考点:1.两个计数原理;2.排列组合的综合问题.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源:2015届河北唐山一中高二下学期期末考试文科数学试卷(解析版) 题型:解答题
已知椭圆 的离心率为
的离心率为 ,过顶点
,过顶点 的直线
的直线 与椭圆
与椭圆 相交于两点
相交于两点 .
.
(1)求椭圆 的方程;
的方程;
(2)若点 在椭圆上且满足
在椭圆上且满足 ,求直线
,求直线 的斜率
的斜率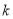 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2015届江西省高二下学期期中考试理科数学试卷(解析版) 题型:解答题
已知曲线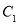 的极坐标方程是
的极坐标方程是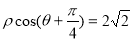 ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为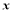 轴的正半轴,建立平面直角坐标系,曲线
轴的正半轴,建立平面直角坐标系,曲线 的参数方程是:
的参数方程是: (
( 是参数).
是参数).
(1)将曲线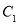 和曲线
和曲线 的方程转化为普通方程;
的方程转化为普通方程;
(2)若曲线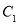 与曲线
与曲线 相交于
相交于 两点,求证
两点,求证 ;
;
(3)设直线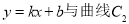 交于两点
交于两点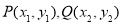 ,且
,且 (
( 且
且 为常数),过弦
为常数),过弦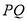 的中点
的中点 作平行于
作平行于 轴的直线交曲线
轴的直线交曲线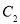 于点
于点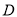 ,求证:
,求证: 的面积是定值.
的面积是定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com