
已知曲线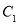 的极坐标方程是
的极坐标方程是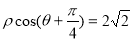 ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为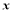 轴的正半轴,建立平面直角坐标系,曲线
轴的正半轴,建立平面直角坐标系,曲线 的参数方程是:
的参数方程是: (
( 是参数).
是参数).
(1)将曲线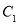 和曲线
和曲线 的方程转化为普通方程;
的方程转化为普通方程;
(2)若曲线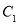 与曲线
与曲线 相交于
相交于 两点,求证
两点,求证 ;
;
(3)设直线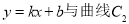 交于两点
交于两点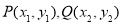 ,且
,且 (
( 且
且 为常数),过弦
为常数),过弦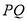 的中点
的中点 作平行于
作平行于 轴的直线交曲线
轴的直线交曲线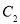 于点
于点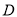 ,求证:
,求证: 的面积是定值.
的面积是定值.
科目:高中数学 来源:2015届河北保定高阳中学、定兴三中高二下学期期末理数学卷(解析版) 题型:选择题
以下说法,正确的个数为( ).
①公安人员由罪犯的脚印的尺寸估计罪犯的身高情况,所运用的是类比推理.
②农谚“瑞雪兆丰年”是通过归纳推理得到的.
③由平面几何中圆的一些性质,推测出球的某些性质这是运用的类比推理.
④个位是5的整数是5的倍数,2375的个位是5,因此2375是5的倍数,这是运用的演绎推理.
A.0 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源:2015届河北保定高阳中学、定兴三中高二下学期期末文数学卷(解析版) 题型:选择题
若奇函数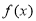 在(0,+∞)上是增函数,又
在(0,+∞)上是增函数,又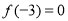 ,则
,则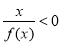 的解集为( ).
的解集为( ).
A.(-3,0)∪(3,+∞) B.(-3,0)∪(0,3)
C.(-∞,-3)∪(3,+∞) D.(-∞,-3)∪(0,3)
查看答案和解析>>
科目:高中数学 来源:2015届河北保定高阳中学、定兴三中高二下学期期末文数学卷(解析版) 题型:选择题
下列函数中,在[1,+∞)上为增函数的是( ).
A.y=(x-2)2 B.y=|x-1| C.y=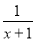 D.y=-(x+1)2
D.y=-(x+1)2
查看答案和解析>>
科目:高中数学 来源:2015届江西省高二下学期期中考试理科数学试卷(解析版) 题型:解答题
6个人坐在一排10个座位上,则(用数字表示).
(1)空位不相邻的坐法有多少种?
(2)4个空位只有3个相邻的坐法有多少种?
(3)4个空位至多有2个相邻的坐法有多少种?
查看答案和解析>>
科目:高中数学 来源:2015届江西省高二下学期期中考试理科数学试卷(解析版) 题型:选择题
函数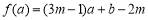 ,当
,当 时,
时,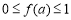 恒成立, 则
恒成立, 则 的最大值与最小值之和为( )
的最大值与最小值之和为( )
A.18 B.16 C.14 D.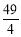
查看答案和解析>>
科目:高中数学 来源:2015届江西省高二下学期期中考试文科数学试卷(解析版) 题型:填空题
记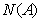 为有限集合
为有限集合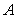 的某项指标,已知
的某项指标,已知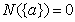 ,
,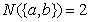 ,
, ,
,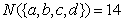 ,运用归纳推理,可猜想出的合理结论是:若
,运用归纳推理,可猜想出的合理结论是:若 ,
, (结果用含
(结果用含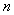 的式子表示).
的式子表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com