
已知△ABC的内角A,B,C满足sin 2A+sin(A-B+C)=sin(C-A-B)+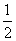 ,面积S满足1≤S≤2,记a,b,c分别为A,B,C所对的边,则下列不等式一定成立的是( )
,面积S满足1≤S≤2,记a,b,c分别为A,B,C所对的边,则下列不等式一定成立的是( )
A.bc(b+c)>8 B.ab(a+b)>16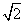
C.6≤abc≤12 D.12≤abc≤24
A [解析] 因为A+B+C=π,所以A+C=π-B,C=π-(A+B),所以由已知等式可得sin 2A+sin(π-2B)=sin[π-2(A+B)]+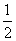 ,即sin 2A+sin 2B=sin 2(A+B)+
,即sin 2A+sin 2B=sin 2(A+B)+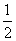 ,
,
所以sin[(A+B)+(A-B)]+sin[(A+B)-(A-B)]=sin 2(A+B)+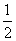 ,
,
所以2 sin(A+B)cos(A-B)=2sin(A+B)cos(A+B)+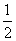 ,
,
所以2sin(A+B)[cos(A-B)-cos(A+B)]=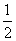 ,所以sin Asin Bsin C=
,所以sin Asin Bsin C=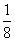 .
.
由1≤S≤2,得1≤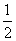 bcsin A≤2.由正弦定理得a=2Rsin A,b=2Rsin B,c=2Rsin C,所以1≤2R2·sin Asin Bsin C≤2,所以1≤
bcsin A≤2.由正弦定理得a=2Rsin A,b=2Rsin B,c=2Rsin C,所以1≤2R2·sin Asin Bsin C≤2,所以1≤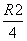 ≤2,即2≤R≤2
≤2,即2≤R≤2 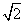 ,所以bc(b+c)>abc=8R3sin Asin Bsin C=R3≥8.
,所以bc(b+c)>abc=8R3sin Asin Bsin C=R3≥8.


科目:高中数学 来源: 题型:
已知a,b,c分别为△ABC三个内角A,B,C的对边,a=2,且(2+b)·(sin A-sin B)=(c-b)sin C,则△ABC面积的最大值为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com