Question

（2011•许昌一模）如图，在直三棱柱ABC-A₁B₁C₁中，AC=3，BC=4，AB=5，AA₁=4，点D是AB的中点，
（1）求证：AC⊥BC₁；
（2）求证：AC₁∥平面CDB₁；
（3）求三棱锥C₁-CDB₁的体积．

Answer 1

分析：（1）先根据AC=3，BC=4，AB=5得到AC⊥BC；再结合其为直棱柱得到AC⊥CC₁，即可证明AC⊥平面BCC₁B₁，进而得到AC⊥BC₁；
（2）先设CB₁与C₁B的交点为E，连接DE；跟怒边长相等得到E为正方形对角线的交点，E为中点；再结合点D是AB的中点可得DE∥AC₁，进而得到AC₁∥平面CDB₁；
（3）直接根据等体积转化，把问题转化为求三棱锥D-C₁CB₁的体积再代入体积计算公式即可．

解答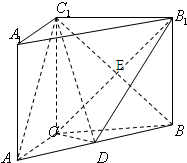：解：（1）直三棱柱ABC-A₁B₁C₁，
底面三边长AC=3，BC=4，AB=5，
∴AB²=AC²+BC²，
∴AC⊥BC．
∵CC₁⊥平面ABC，AC?平面ABC，
∴AC⊥CC₁，又BC∩CC₁=C．
∴AC⊥平面BCC₁B₁，BC₁?平面B₁C₁CB，
∴AC⊥BC₁…（5分）
（2）设CB₁与C₁B的交点为E，连接DE，
因为；BC=AA₁=4，
所以BCC₁B₁为正方形，
故E是C₁B的中点，
∵D是AB的中点，E是C₁B的中点，
∴DE∥AC₁，
∵DE?平面CDB₁，AC₁?平面CDB₁，
∴AC₁∥平面CDB₁．．     …（10分）
（3）因为AC⊥平面BCC₁B₁，，D为中点
所以D到平面BCC₁B₁的距离等于

1

2

AC，
∵VC1-CDB 1
=VD-B 1C 1C 
=

1

3

S△B 1C 1C •

1

2

AC
=

1

3

×（

1

2

×4×4）×

1

2

×3
=4．…（14分）

点评：本题是对立体几何知识的综合考查．一般在求三棱锥的体积直接不好找时，常用等体积转化求解．（转化为高好找的三棱锥）