有六种不同颜色,给如图的六个区域涂色,要求相邻区域不同色,不同的涂色方法共有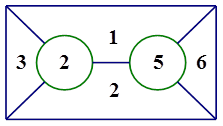A．4320 B．2880 C．1440 D．720 题目和参考答案——青夏教育精英家教网—

有六种不同颜色,给如图的六个区域涂色,要求相邻区域不同色,不同的涂色方法共有( )

A．4320

B．2880

C．1440

D．720

解析试题分析：第一个区域有6种不同的涂色方法，第二个区域有5种不同的涂色方法，第三个区域有4种不同的涂色方法，第四个区域有3种不同的涂色方法，第六个区域有4种不同的涂色方法，第五个区域有3种不同的涂色方法，根据乘法原理，故选：A．
考点：乘法原理.

练习册系列答案

开心快乐假期作业暑假作业西安出版社系列答案

学业考试综合练习册系列答案

名题训练系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：解答题

(12分)学校游园活动有这样一个游戏项目：甲箱子里装有3个白球、2个黑球，乙箱子里装有1个白球、2个黑球，这些球除颜色外完全相同，每次游戏从这两个箱子里各随机摸出2个球，若摸出的白球不少于2个，则获奖．（每次游戏结束后将球放回原箱）
（1）求在1次游戏中，①摸出3个白球的概率；②获奖的概率；（6分）
（2）求在2次游戏中获奖次数X的分布列及数学期望E（X）. （6分）

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

某校教务处要对高三上学期期中数学试卷进行调研，考察试卷中某道填空题的得分情况.已知该题有两空，第一空答对得3分，答错或不答得0分；第二空答对得2分，答错或不答得0分.第一空答对与否与第二空答对与否是相互独立的.从该校1468份试卷中随机抽取1000份试卷，其中该题的得分组成容量为1000的样本，统计结果如下表：

第一空得分情况			第二空得分情况
得分	0	3	得分	0	2
人数	198	802	人数	698	302

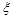（Ⅰ）求样本试卷中该题的平均分，并据此估计该校高三学生该题的平均分.
（Ⅱ）该校的一名高三学生因故未参加考试，如果这名学生参加考试，以样本中各种得分情况的频率（精确到0.1）作为该同学相应的各种得分情况的概率.试求该同学这道题得分

的数学期望.

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

（本小题满分12分）一个口袋内装有形状、大小相同的2个白球和3个黑球。
（1）从中随机地摸出一个球不放回，再随机地摸出一个球，求两球同时是黑球的概率；
（2）从中随机地摸出一个球，放回后再随机地摸出一个球，求两球颜色恰好不同的概率

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

（本题满分13分）
检测部门决定对某市学校教室的空气质量进行检测，空气质量分为A、B、C三级．
每间教室的检测方式如下：分别在同一天的上、下午各进行一次检测，若两次检测中有C级或两次都是B级，则该教室的空气质量不合格．设各教室的空气质量相互独立，且每次检测的结果也相互独立．根据多次抽检结果，一间教室一次检测空气质量为A、B、C三级的频率依次为，，.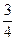
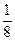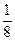(1) 在该市的教室中任取一间，估计该间教室空气质量合格的概率；
(2) 如果对该市某中学的4间教室进行检测，记在上午检测空气质量为A级的教室间数为X，并以空气质量为A级的频率作为空气质量为A级的概率，求X的分布列及期望值．