思路分析:可设两条高线交于一点,只要证明第三条高也过此点即可.
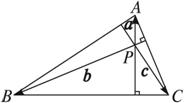
证明:如图,设△ABC的BC、CA两边上的高交于点P.再证PC⊥AB.
设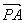 =a,
=a, =b,
=b,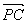 =c,则
=c,则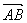 =b-a,
=b-a, =c-b,
=c-b,  =a-c.
=a-c.
∵ ⊥
⊥ ,
, ⊥
⊥ ,
,
∴a·(c-b)=0,
即a·c=a·b;b·(a-c)=0,
即a·b=b·c.
从而a·c=b·c,
即c·(b-a)=0.
所以 ⊥
⊥ ,即PC⊥AB.
,即PC⊥AB.
这就证明了点P在△ABC的第三边AB的高线上,所以△ABC的三条高线交于一点.
方法归纳 证明三线共点,常变换思维方式,以减少思维量.对于垂直这种特殊情况常先借助向量垂直的充要条件,再进一步进行向量运算来解决问题.
