Question

用向量法证明三角形的三条中线交于一点.

Answer 1

思路分析：解决本题有两个关键点:一是由题意证明三线交于一点,需先明确要用同一法;二是利用向量证明两点重合的方法是构造以同一点为起点,这两点为终点的两向量相等,从而得这两点重合.

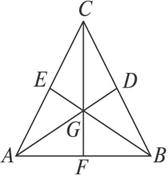
证明:设D、E、F分别是△ABC的三边BC、AC、AB的中点,

令=a,=b为基底,

则=a-b,=a-b,=-a+b,

设AD与BE交于点G₁,且=λ,=μ,

则有=λa-b,=-a+μb.

又有=+=(1-)a+(μ-1)b,

∴

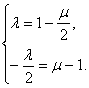
解得λ=μ=,

∴=,

再设与交于G₂,

同理求得=,

∴G₁点、G₂点重合,即AD、BE、CF交于一点.

∴三角形三条中线交于一点.

温馨提示

    平面向量基本定理是向量法的理论基础,这个定理揭示了平面向量是由平面内两个不共线向量“生成”的,或者说,任一平面向量均可用平面内的任意两个不共线向量线性表示的实质,它不仅提供了向量的几何表示方法,同时也使向量用坐标来表示成为可能,从而架起了向量的几何运算与代数运算之间的桥梁.如我们已经证明过的结论:若A、B是直线l上任意两点,O是l外一点,则对直线l上任一点P,存在实数t,使OP关于基底{,}的分解式为=(1-t) +t(*)并且满足(*)式中点P一定在l上.

    实际上,向量等式(*)叫做直线l的向量参数方程式,其中实数t叫做参变数,简称参数.