
【题目】已知![]() ,函数
,函数![]() .
.
(1)求证:曲线![]() 在点
在点![]() 处的切线过定点;
处的切线过定点;
(2)若![]() 是
是![]() 在区间
在区间![]() 上的极大值,但不是最大值,求实数
上的极大值,但不是最大值,求实数![]() 的取值范围;
的取值范围;
(3)求证:对任意给定的正数![]() ,总存在
,总存在![]() ,使得
,使得![]() 在
在![]() 上为单调函数.
上为单调函数.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn满足![]() ,
,
(1)求数列{an}的通项公式;
(2)求证:数列{an}中的任意三项不可能成等差数列;
(3)设![]() ,Tn为{bn}的前n项和,求证
,Tn为{bn}的前n项和,求证![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知一个八面体各棱长均为1,四边形ABCD为正方形,则下列命题中不正确的是
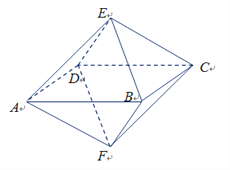
A. 不平行的两条棱所在直线所成的角为![]() 或
或![]() B. 四边形AECF为正方形
B. 四边形AECF为正方形
C. 点A到平面BCE的距离为![]() D. 该八面体的顶点在同一个球面上
D. 该八面体的顶点在同一个球面上
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以原点
中,以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() ,
, ![]() 极坐标方程分别为
极坐标方程分别为![]() ,
, ![]() .
.
(Ⅰ)![]() 和
和![]() 交点的极坐标;
交点的极坐标;
(Ⅱ)直线![]() 的参数方程为
的参数方程为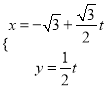 (
(![]() 为参数),
为参数),![]() 与
与![]() 轴的交点为
轴的交点为![]() ,且与
,且与![]() 交于
交于![]() ,
, ![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某房屋开发公司根据市场调查,计划在2017年开发的楼盘中设计“特大套”、“大套”、“经济适
用房”三类商品房,每类房型中均有舒适和标准两种型号.某年产量如下表:
房型 | 特大套 | 大套 | 经济适用房 |
舒适 | 100 | 150 |
|
标准 | 300 |
| 600 |
若按分层抽样的方法在这一年生产的套房中抽取50套进行检测,则必须抽取“特大套”套房10套, “大套”15套.
(1)求![]() ,
,![]() 的值;
的值;
(2)在年终促销活动中,奖给了某优秀销售公司2套舒适型和3套标准型“经济适用型”套房,该销售公司又从中随机抽取了2套作为奖品回馈消费者.求至少有一套是舒适型套房的概率;
(3)今从“大套”类套房中抽取6套,进行各项指标综合评价,并打分如下:
![]()
现从上面6个分值中随机的一个一个地不放回抽取,规定抽到数9.6或9.7,抽取工作即停止.记在抽取到数9.6或9.7所进行抽取的次数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产的一种产品的广告费用![]() (单位:万元)与销售额
(单位:万元)与销售额![]() (单位:万元)的统计数据如下表:
(单位:万元)的统计数据如下表:
广告费用 |
|
|
|
|
|
销售额 |
|
|
|
|
|
(1)根据上述数据,求出销售额![]() (万元)关于广告费用
(万元)关于广告费用![]() (万元)的线性回归方程;
(万元)的线性回归方程;
(2)如果企业要求该产品的销售额不少于![]() 万元,则投入的广告费用应不少于多少万元?
万元,则投入的广告费用应不少于多少万元?
(参考数值: ![]() .
.
回归直线的斜率和截距的最小二乘法估计公式分别为: 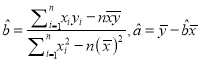 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com