
分析 (Ⅰ)记“该考生至少答对一题”为事件A,Ai为事件“答对第i题”,i=1,2,3,由事件的独立性和互斥性,利用对立事件概率计算公式能求出该考生至少答对一道题的概率.
(Ⅱ)由已知得X的可能取值为0,5,10,15,分别求出相应的概率,由此能求出X的分布列和EX.
解答 解:(Ⅰ)记“该考生至少答对一题”为事件A,Ai为事件“答对第i题”,i=1,2,3,
由事件的独立性和互斥性,得:
P(A)=1-P($\overline{A}$)=1-$P(\overline{{A}_{1}})P(\overline{{A}_{2}})P(\overline{{A}_{3}})$
=1-$\frac{2}{5}×\frac{1}{2}×\frac{3}{5}$=$\frac{22}{25}$.
(Ⅱ)由已知得X的可能取值为0,5,10,15,
P(X=0)=P($\overline{{A}_{1}}$)P($\overline{{A}_{2}}$)P($\overline{{A}_{3}}$)=$\frac{2}{5}×\frac{1}{2}×\frac{3}{5}=\frac{6}{50}$,
P(X=5)=P(${A}_{1}\overline{{A}_{2}}\overline{{A}_{3}}$+$\overline{{A}_{1}}{A}_{2}\overline{{A}_{3}}$+$\overline{{A}_{1}}\overline{{A}_{2}}{{A}_{3}}^{\;}$)
=$\frac{3}{5}×\frac{1}{2}×\frac{3}{5}$+$\frac{2}{5}×\frac{1}{2}×\frac{3}{5}$+$\frac{2}{5}×\frac{1}{2}×\frac{2}{5}$=$\frac{19}{50}$,
P(X=10)=P(${A}_{1}{A}_{2}\overline{{A}_{3}}$+${A}_{1}\overline{{A}_{2}}{A}_{3}$+${A}_{1}{A}_{2}\overline{{A}_{3}}$)
=$\frac{3}{5}×\frac{1}{2}×\frac{3}{5}+\frac{3}{5}×\frac{1}{2}×\frac{2}{5}$+$\frac{2}{5}×\frac{1}{2}×\frac{2}{5}$=$\frac{19}{50}$,
P(X=15)=P(A1A2A3)=$\frac{3}{5}×\frac{1}{2}×\frac{2}{5}=\frac{6}{50}$,
∴X的分布列为:
| X | 0 | 5 | 10 | 15 |
| P | $\frac{6}{50}$ | $\frac{19}{50}$ | $\frac{19}{50}$ | $\frac{6}{50}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意对立事件的概率计算公式的合理运用.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{4}$ | B. | $\frac{4}{5}$ | C. | $\frac{4}{3}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
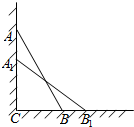 如图,一根木棒AB长为2米,斜靠在墙壁AC上,∠ABC=60°,若AB滑动至A1B1位置,且$A{A_1}=(\sqrt{3}-\sqrt{2})$米,则①BB1=$\sqrt{2}$-1米;②木棒AB的中点D所经过的路程为$\frac{π}{12}$米.
如图,一根木棒AB长为2米,斜靠在墙壁AC上,∠ABC=60°,若AB滑动至A1B1位置,且$A{A_1}=(\sqrt{3}-\sqrt{2})$米,则①BB1=$\sqrt{2}$-1米;②木棒AB的中点D所经过的路程为$\frac{π}{12}$米.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a2<b2 | B. | $\frac{1}{{a{b^2}}}$<$\frac{1}{{{a^2}b}}$ | C. | a2b<ab2 | D. | $\frac{b}{a}$<$\frac{a}{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
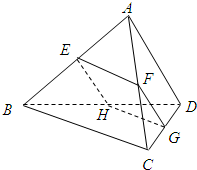 如图,空间四边形ABCD的对棱AD、BC成90°的角,且AD=BC=a,平行于AD与BC的截面分别交AB、AC、CD、BD于E、F、G、H.E在AB上,截面EGFH的最大面积是$\frac{1}{4}{a}^{2}$.
如图,空间四边形ABCD的对棱AD、BC成90°的角,且AD=BC=a,平行于AD与BC的截面分别交AB、AC、CD、BD于E、F、G、H.E在AB上,截面EGFH的最大面积是$\frac{1}{4}{a}^{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com