
已知直线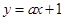 与双曲线
与双曲线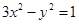 交于
交于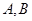 两点,
两点,
(1)若以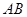 线段为直径的圆过坐标原点,求实数
线段为直径的圆过坐标原点,求实数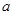 的值。
的值。
(2)是否存在这样的实数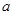 ,使
,使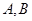 两点关于直线
两点关于直线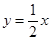 对称?说明理由.
对称?说明理由.
(1)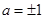 (2)不存在这样的a,使A(
(2)不存在这样的a,使A(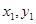 ),B(
),B(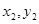 )关于直线
)关于直线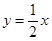 对称
对称
【解析】
试题分析:(1)联立方程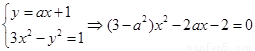 ,
,
设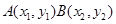 ,那么:
,那么: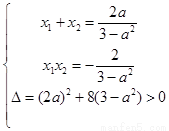
由于以AB线段为直径的圆经过原点,那么: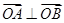 ,即
,即 。
。
所以: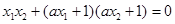 ,得到:
,得到: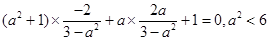 ,解得
,解得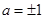 6分
6分
(2)假定存在这样的a,使A(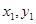 ),B(
),B(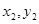 )关于直线
)关于直线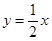 对称。
对称。
那么: ,两式相减得:
,两式相减得: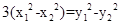 ,从而
,从而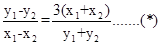
因为A(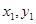 ),B(
),B(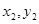 )关于直线
)关于直线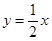 对称,所以
对称,所以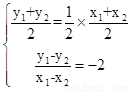
代入(*)式得到:-2=6,矛盾。
也就是说:不存在这样的a,使A(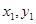 ),B(
),B(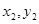 )关于直线
)关于直线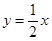 对称。 13分
对称。 13分
考点:直线与双曲线的位置关系
点评:第一问中首先将以AB为直径的圆经过原点转化为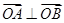 ,进而可用点的坐标表示,第二问中把握好对称的两个条件:A,B的中点在直线上,过A,B两点的直线与已知直线互相垂直
,进而可用点的坐标表示,第二问中把握好对称的两个条件:A,B的中点在直线上,过A,B两点的直线与已知直线互相垂直


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源:2010年河北省邯郸市高二上学期期末考试数学理卷 题型:解答题
(示范高中做)(本题满分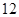 分)已知双曲线
分)已知双曲线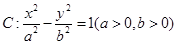 的离心率为
的离心率为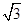 ,且双曲线上点到右焦点的距离与到直线
,且双曲线上点到右焦点的距离与到直线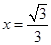 的距离之比为
的距离之比为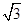
(1) 求双曲线 的方程;
的方程;
(2)已知直线 与双曲线
与双曲线 交于不同的两点
交于不同的两点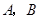 ,且线段
,且线段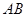 的中点在圆
的中点在圆 上,求
上,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2010年山西省高二下学期期中考试数学(文) 题型:解答题
(本小题满分12分)
已知直线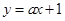 与双曲线
与双曲线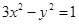 交于A、B两点,
交于A、B两点,
(1)若以AB线段为直径的圆过坐标原点,求实数a的值。
(2)是否存在这样的实数a,使A、B两点关于直线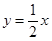 对称?说明理由.
对称?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com