
在锐角△ABC中,a、b、c分别为∠A、∠B、∠C所对的边,且 a=2csinA.
a=2csinA.
(1)确定∠C的大小;
(2)若c= ,求△ABC周长的取值范围.
,求△ABC周长的取值范围.
(1)∠C=60°;(2)(3+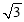 ,3
,3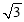 ].
].
【解析】
试题分析:
(1)把已知的等式利用正弦定理化简,变形为: sinA=2sinCsinA,根据sinA不为0,可得出sinC的值,由三角形为锐角三角形,得出C为锐角,利用特殊角的三角函数值即可求出C的度数;
sinA=2sinCsinA,根据sinA不为0,可得出sinC的值,由三角形为锐角三角形,得出C为锐角,利用特殊角的三角函数值即可求出C的度数;
(2)由c及sinC的值,利用正弦定理列出关系式,得到a=2sinA,b=2sinB,表示出三角形的周长,将表示出a,b及c的值代入,由C的度数,求出A+B的度数,用A表示出B,把B也代入表示出的周长,利用两角和与差的正弦函数公式及特殊角的三角函数值整理后,提取2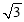 再利用两角和与差的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,根据A为锐角,得到A的范围,进而确定出这个角的范围,根据正弦函数的图象与性质求出此时正弦函数的值域,即可确定出周长的范围.
再利用两角和与差的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,根据A为锐角,得到A的范围,进而确定出这个角的范围,根据正弦函数的图象与性质求出此时正弦函数的值域,即可确定出周长的范围.
试题解析:(1)已知a、b、c分别为∠A、∠B、∠C所对的边,由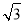 a=2csinA,
a=2csinA,
得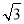 sinA=2sinCsinA,又sinA≠0,则sinC=
sinA=2sinCsinA,又sinA≠0,则sinC=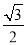 ,∴∠C=60°或∠C=120°,
,∴∠C=60°或∠C=120°,
∵△ABC为锐角三角形,∴∠C=120°舍去。∴∠C=60°.
(2)∵c=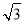 ,sinC=
,sinC=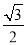
∴由正弦定理得: ,
,
即a=2sinA,b=2sinB,又A+B=π-C=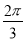 ,即B=
,即B=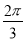 -A,
-A,
∴a+b+c=2(sinA+sinB)+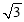
=2[sinA+sin(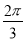 -A)]+
-A)]+ 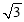
=2(sinA+sin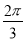 cosA-cos
cosA-cos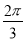 sinA)+
sinA)+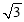
=3sinA+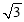 cosA+
cosA+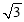
=2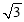 (sinAcos
(sinAcos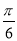 +cosAsin
+cosAsin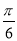 )+
)+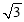
=2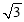 sin(A+
sin(A+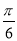 )+
)+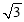 ,
,
∵△ABC是锐角三角形,
∴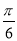 <∠A<
<∠A<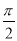 ,
,
∴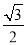 <sin(A+
<sin(A+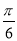 )≤1,
)≤1,
则△ABC周长的取值范围是(3+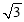 ,3
,3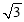 ].
].
考点:正弦定理;正弦函数的定义域和值域.


科目:高中数学 来源:2014年高考数学三轮冲刺模拟 三角函数、解三角形与平面向量(解析版) 题型:选择题
已知f(x)是定义在R上的偶函数,且以2为周期,则“f(x)为[0,1]上的增函数”是“f(x)为[3,4]上的减函数”的( )
A.既不充分也不必要的条件
B.充分而不必要的条件
C.必要而不充分的条件
D.充要条件
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河北省邯郸市高二第一次调研数学试卷(解析版) 题型:选择题
在△ABC中,AB=5,BC=7,AC=8,则 的值为( )
的值为( )
A.79 B.69 C.5 D.-5
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省高二上学期开学考试数学试卷(解析版) 题型:填空题
已知某个几何体的三视图如下(主视图的弧线是半圆),根据图中标出的尺寸(单位:cm),可得这个几何体的体积是 .

查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨选修4-4第3课时练习卷(解析版) 题型:解答题
若关于实数x的不等式|x-5|+|x+3|<a无解,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com