在公差为d(d≠0)的等差数列{an}和公比为q的等比数列{bn}中,已知a1=b1=1,a2=b2,a8=b3.
(Ⅰ)求数列{an}与{bn}的通项公式;
(Ⅱ)是否存在常数a,b,使得对于一切正整数n,都有an=logabn+b成立?若存在,求出常数a和b,若不存在说明理由.
解:(Ⅰ)由条件得:
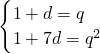
∴
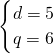
,
∴a
n=5n-4,
b
n=6
n-1.
(Ⅱ)假设存在a,b使a
n=log
ab
n+b成立,
则5n-4=log
a6
n-1+b,
∴5n-4=(n-1)log
a6+b,
∴(5-log
a6)n+(log
a6-b-4)=0对一切正整数恒成立.
∴
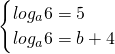
,
既
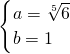
.
故存在常数
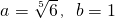
,
使得对于n∈N
*时,都有a
n=log
ab
n+b恒成立.…(12分)
分析:(Ⅰ)由条件得:
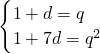
,由此能求出求结果.
(Ⅱ)假设存在a,b使a
n=log
ab
n+b成立,则5n-4=log
a6
n-1+b?5n-4=(n-1)log
a6+b?(5-log
a6)n+(log
a6-b-4)=0对一切正整数恒成立.由此能求出存在常数
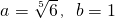
使得对于n∈N
*时,都有a
n=log
ab
n+b恒成立.
点评:本题首先考查等差数列、等比数列的基本量、通项,结合含两个变量的不等式的处理问题,对数学思维的要求比较高,要求学生理解“存在”、“恒成立”,以及运用一般与特殊的关系进行否定,本题有一定的探索性.综合性强,难度大,易出错.

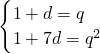
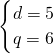 ,
,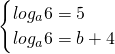 ,
,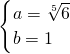 .
.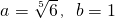 ,
,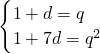 ,由此能求出求结果.
,由此能求出求结果.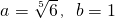 使得对于n∈N*时,都有an=logabn+b恒成立.
使得对于n∈N*时,都有an=logabn+b恒成立.
