
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若![]() 对
对![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:
【题目】点![]() 分别是正方体
分别是正方体![]() 的棱
的棱![]() 的中点,如图所示,则下列命题中的真命题是________(写出所有真命题的编号).
的中点,如图所示,则下列命题中的真命题是________(写出所有真命题的编号).
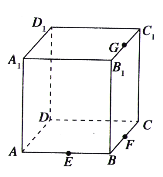
①以正方体的顶点为顶点的三棱锥的四个面中最多只有三个面是直角三角形;②点![]() 在直线
在直线![]() 上运动时,总有
上运动时,总有![]() ;③点
;③点![]() 在直线
在直线![]() 上运动时,三棱锥
上运动时,三棱锥![]() 的体积的定值;④若点
的体积的定值;④若点![]() 是正方体的面
是正方体的面![]() 内的一动点,且
内的一动点,且![]() 到点
到点![]() 和
和![]() 距离相等,则点
距离相等,则点![]() 的轨迹是一条线段.
的轨迹是一条线段.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数y=f(x)为偶函数,求k 的值;
(2)求函数y=f(x)在区间[0,4]上的最大值;
(3)若方程f(x)=0 有且仅有一个根,求实数k 的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三课外兴趣小组为了解高三同学高考结束后是否打算观看2018年足球世界杯比赛的情况,从全校高三年级1500名男生、1000名女生中按分层抽样的方式抽取125名学生进行问卷调查,情况如下表:
打算观看 | 不打算观看 | |
女生 | 20 | b |
男生 | c | 25 |
(1)求出表中数据b,c;
(2)判断是否有99%的把握认为观看2018年足球世界杯比赛与性别有关;
(3)为了计算“从10人中选出9人参加比赛”的情况有多少种,我们可以发现它与“从10人中选出1人不参加比赛”的情况有多少种是一致的.现有问题:在打算观看2018年足球世界杯比赛的同学中有5名男生、2名女生来自高三(5)班,从中推选5人接受校园电视台采访,请根据上述方法,求被推选出的5人中恰有四名男生、一名女生的概率.
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 |
K0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
附: 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一只红铃虫的产卵数y和温度x有关,现收集了6组观测数据于下表中,通过散点图可以看出样本点分布在一条指数型函数y=![]() 的图象的周围.
的图象的周围.
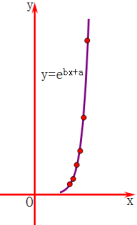
(1)试求出y关于x的上述指数型的回归曲线方程(结果保留两位小数);
(2)试用(1)中的回归曲线方程求相应于点(24,17)的残差![]() .(结果保留两位小数)
.(结果保留两位小数)
温度x(°C) | 20 | 22 | 24 | 26 | 28 | 30 |
产卵数y(个) | 6 | 9 | 17 | 25 | 44 | 88 |
z=lny | 1.79 | 2.20 | 2.83 | 3.22 | 3.78 | 4.48 |
几点说明:
①结果中的![]() 都应按题目要求保留两位小数.但在求
都应按题目要求保留两位小数.但在求![]() 时请将
时请将![]() 的值多保留一位即用保留三位小数的结果代入.
的值多保留一位即用保留三位小数的结果代入.
②计算过程中可能会用到下面的公式:回归直线方程的斜率![]() =
= =
= ,截距
,截距![]() .
.
③下面的参考数据可以直接引用:![]() =25,
=25,![]() =31.5,
=31.5,![]() ≈3.05,
≈3.05,![]() =5248,
=5248,![]() ≈476.08,
≈476.08,![]() ,ln18.17≈2.90.
,ln18.17≈2.90.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为净化新安江水域的水质,市环保局于2017年底在新安江水域投入一些蒲草,这些蒲草在水中的蔓延速度越来越快,2018年二月底测得蒲草覆盖面积为![]() ,2018年三月底测得覆盖面积为
,2018年三月底测得覆盖面积为![]() ,蒲草覆盖面积
,蒲草覆盖面积![]() (单位:
(单位:![]() )与月份
)与月份![]() (单位:月)的关系有两个函数模型
(单位:月)的关系有两个函数模型![]() 与
与![]() 可供选择.
可供选择.
(Ⅰ)分别求出两个函数模型的解析式;
(Ⅱ)若市环保局在2017年年底投放了![]() 的蒲草,试判断哪个函数模型更合适?并说明理由;
的蒲草,试判断哪个函数模型更合适?并说明理由;
(Ⅲ)利用(Ⅱ)的结论,求蒲草覆盖面积达到![]() 的最小月份.
的最小月份.
(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com