
【题目】点![]() 分别是正方体
分别是正方体![]() 的棱
的棱![]() 的中点,如图所示,则下列命题中的真命题是________(写出所有真命题的编号).
的中点,如图所示,则下列命题中的真命题是________(写出所有真命题的编号).
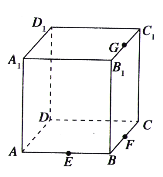
①以正方体的顶点为顶点的三棱锥的四个面中最多只有三个面是直角三角形;②点![]() 在直线
在直线![]() 上运动时,总有
上运动时,总有![]() ;③点
;③点![]() 在直线
在直线![]() 上运动时,三棱锥
上运动时,三棱锥![]() 的体积的定值;④若点
的体积的定值;④若点![]() 是正方体的面
是正方体的面![]() 内的一动点,且
内的一动点,且![]() 到点
到点![]() 和
和![]() 距离相等,则点
距离相等,则点![]() 的轨迹是一条线段.
的轨迹是一条线段.
 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
【题目】【2018河南濮阳市高三一模】已知点![]() 在抛物线
在抛物线![]() 上,
上, ![]() 是抛物线上异于
是抛物线上异于![]() 的两点,以
的两点,以![]() 为直径的圆过点
为直径的圆过点![]() .
.
(I)证明:直线![]() 过定点;
过定点;
(II)过点![]() 作直线
作直线![]() 的垂线,求垂足
的垂线,求垂足![]() 的轨迹方程.
的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直线![]() 的参数方程是
的参数方程是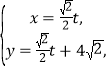 (
(![]() 是参数),圆
是参数),圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求圆心![]() 的直角坐标;
的直角坐标;
(Ⅱ)由直线![]() 上的点向圆
上的点向圆![]() 引切线,求切线长的最小值.
引切线,求切线长的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的顶点为平面直角坐标系
的顶点为平面直角坐标系![]() 的坐标原点
的坐标原点![]() ,焦点为圆
,焦点为圆![]() 的圆心
的圆心![]() .经过点
.经过点![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() 两点,交圆
两点,交圆![]() 于
于![]() 两点,
两点,![]() 在第一象限,
在第一象限,![]() 在第四象限.
在第四象限.
(1)求抛物线![]() 的方程;
的方程;
(2)是否存在直线![]() 使
使![]() 是
是![]() 与
与![]() 的等差中项?若存在,求直线
的等差中项?若存在,求直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(1)已知![]() 的解集为
的解集为![]() ,求实数
,求实数![]() 的值;
的值;
(2)已知![]() ,设
,设![]() 、
、![]() 是关于
是关于![]() 的方程
的方程![]() 的两根,且
的两根,且![]() ,求实数
,求实数![]() 的值;
的值;
(3)已知![]() 满足
满足![]() ,且关于
,且关于![]() 的方程
的方程![]() 的两实数根分别在区间
的两实数根分别在区间![]() 内,求实数
内,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在矩形![]() 中,AB=2AD,
中,AB=2AD,![]() 为DC的中点,将△ADM沿AM折起使平面ADM⊥平面ABCM.
为DC的中点,将△ADM沿AM折起使平面ADM⊥平面ABCM.
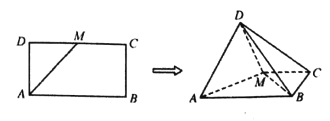
(1)当AB=2时,求三棱锥![]() 的体积;
的体积;
(2)求证:BM⊥AD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中![]() 中,直线
中,直线![]() ,圆
,圆![]() 的参数方程为
的参数方程为![]() 为参数),以坐标原点为极点,以
为参数),以坐标原点为极点,以![]() 轴正半轴为极轴,建立极坐标系.
轴正半轴为极轴,建立极坐标系.
(1)求直线![]() 和圆
和圆![]() 的极坐标方程;
的极坐标方程;
(2)若直线![]() 与圆
与圆![]() 交于
交于![]() 两点,且
两点,且![]() 的面积是
的面积是![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com