
【题目】【2018河南濮阳市高三一模】已知点![]() 在抛物线
在抛物线![]() 上,
上, ![]() 是抛物线上异于
是抛物线上异于![]() 的两点,以
的两点,以![]() 为直径的圆过点
为直径的圆过点![]() .
.
(I)证明:直线![]() 过定点;
过定点;
(II)过点![]() 作直线
作直线![]() 的垂线,求垂足
的垂线,求垂足![]() 的轨迹方程.
的轨迹方程.
【答案】(I)证明见解析;(II)![]() .
.
【解析】试题分析:(1)代入点的坐标得到抛物线方程![]() ,设直线
,设直线![]() ,与抛物线方程联立,得到根与系数的关系,利用
,与抛物线方程联立,得到根与系数的关系,利用![]() ,代入根与系数的关系,求得
,代入根与系数的关系,求得![]() ,代入直线方程,得到定点;(2)根据(1)可知,点
,代入直线方程,得到定点;(2)根据(1)可知,点![]() 的轨迹满足圆的方程,以
的轨迹满足圆的方程,以![]() 为直径的圆去掉
为直径的圆去掉![]() ,写出圆的方程即可.
,写出圆的方程即可.
试题解析:(1)点![]() 在抛物线
在抛物线![]() 上,代入得
上,代入得![]() ,所以抛物线
,所以抛物线![]() 的方程为
的方程为![]() ,
,
由题意知,直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程为
的方程为![]() ,设
,设![]() ,
, ![]() ,
,
联立得![]() ,得
,得![]() ,
, ![]() ,
,
由于![]() ,所以
,所以![]() ,即
,即![]() ,
,
即![]() .(*)
.(*)
又因为![]() ,
, ![]() ,
,
代入(*)式得![]() ,即
,即![]() ,
,
所以![]() 或
或![]() ,即
,即![]() 或
或![]() .
.
当![]() 时,直线
时,直线![]() 方程为
方程为![]() ,恒过定点
,恒过定点![]() ,
,
经验证,此时![]() ,符合题意;
,符合题意;
当![]() 时,直线
时,直线![]() 方程为
方程为![]() ,恒过定点
,恒过定点![]() ,不合题意,
,不合题意,
所以直线![]() 恒过定点
恒过定点![]() .
.
(2)由(1),设直线![]() 恒过定点
恒过定点![]() ,则点
,则点![]() 的轨迹是以
的轨迹是以![]() 为直径的圆且去掉
为直径的圆且去掉![]() ,方程为
,方程为![]() .
.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】某镇在政府“精准扶贫”的政策指引下,充分利用自身资源,大力发展养殖业,以增加收入,政府计划共投入72万元,全部用于甲、乙两个合作社,每个合作社至少要投入15万元,其中甲合作社养鱼,乙合作社养鸡,在对市场进行调研分析发现养鱼的收益M、养鸡的收益N与投入a(单位:万元)满足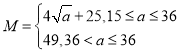 ,N=
,N=![]() a+20.设甲合作社的投入为x(单位:万元),两个合作社的总收益为f(x)(单位:万元).
a+20.设甲合作社的投入为x(单位:万元),两个合作社的总收益为f(x)(单位:万元).
(1)当甲合作社的投入为25万元时,求两个合作社的总收益;
(2)试问如何安排甲、乙两个合作社的投入,才能使总收益最大,最大总收益为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为创建国家级文明城市,某城市号召出租车司机在高考期间至少参加一次“爱心送考”,该城市某出租车公司共200名司机,他们参加“爱心送考”的次数统计如图所示.
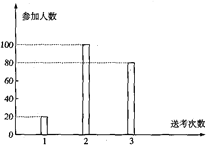
(1)求该出租车公司的司机参加“爱心送考”的人均次数;
(2)从这200名司机中任选两人,设这两人参加送考次数之差的绝对值为随机变量![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司计划投资A、B两种金融产品,根据市场调查与预测,A产品的利润与投资量成正比例,其关系如图1,B产品的利润与投资量的算术平方根成正比例,其关系如图2(注:利润与投资量的单位:万元).
(1)分别将A、B两产品的利润表示为投资量的函数关系式;
(2)该公司已有10万元资金,并全部投入A、B两种产品中,问:怎样分配这10万元投资,才能使公司获得最大利润?其最大利润为多少万元?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医药研究所开发的一种新药,如果成年人按规定的剂量服用,据监测:服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线.

(1)写出第一次服药后,y与t之间的函数关系式y=f(t);
(2)据进一步测定:每毫升血液中含药量不少于0.25微克时,治疗有效.求服药一次后治疗有效的时间是多长?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() ,其中
,其中![]() ,焦距为2,过点
,焦距为2,过点![]() 的直线l与椭圆C交于点A,B,点B在A,M之间.又线段AB的中点的横坐标为
的直线l与椭圆C交于点A,B,点B在A,M之间.又线段AB的中点的横坐标为![]() ,且
,且![]() .
.
(1)求椭圆C的标准方程.
(2)求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】点![]() 分别是正方体
分别是正方体![]() 的棱
的棱![]() 的中点,如图所示,则下列命题中的真命题是________(写出所有真命题的编号).
的中点,如图所示,则下列命题中的真命题是________(写出所有真命题的编号).
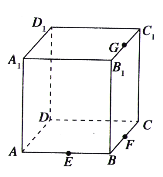
①以正方体的顶点为顶点的三棱锥的四个面中最多只有三个面是直角三角形;②点![]() 在直线
在直线![]() 上运动时,总有
上运动时,总有![]() ;③点
;③点![]() 在直线
在直线![]() 上运动时,三棱锥
上运动时,三棱锥![]() 的体积的定值;④若点
的体积的定值;④若点![]() 是正方体的面
是正方体的面![]() 内的一动点,且
内的一动点,且![]() 到点
到点![]() 和
和![]() 距离相等,则点
距离相等,则点![]() 的轨迹是一条线段.
的轨迹是一条线段.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com