
【题目】某医药研究所开发的一种新药,如果成年人按规定的剂量服用,据监测:服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线.

(1)写出第一次服药后,y与t之间的函数关系式y=f(t);
(2)据进一步测定:每毫升血液中含药量不少于0.25微克时,治疗有效.求服药一次后治疗有效的时间是多长?
【答案】(1)![]() ; (2)服药一次后治疗有效的时间是5-
; (2)服药一次后治疗有效的时间是5-![]() =
=![]() 小时.
小时.
【解析】
(1)由函数图象的奥这是一个分段函数,第一段为正比例函数的一段,第二段是指数函数的一段,由于两端函数均过点![]() ,代入点
,代入点![]() 的坐标,求出参数的值,即可得到函数的解析式;
的坐标,求出参数的值,即可得到函数的解析式;
(2)由(1)的结论将函数值![]() 代入函数的解析式,构造不等式,求出每毫升血液中函数不少于
代入函数的解析式,构造不等式,求出每毫升血液中函数不少于![]() 微克的起始时刻和结束时刻,即可得到结论.
微克的起始时刻和结束时刻,即可得到结论.
(1)由题意,根据给定的函数的图象,可设函数的解析式为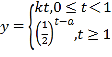 ,
,
又由函数的图象经过点![]() ,
,
则当![]() 时,
时,![]() ,解得
,解得![]() ,
,
又由![]() 时,
时,![]() ,解得
,解得![]() ,
,
所以函数的解析式为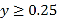 .
.
(2)由题意,令![]() ,即当
,即当![]() 时,
时,![]() ,解得
,解得![]() ,
,
当![]() 时,
时,![]() ,解得
,解得![]() ,
,
综上所述,可得实数![]() 的取值范围是
的取值范围是![]() ,
,
所以服药一次后治疗有效的时间是![]() 小时.
小时.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知点![]() 是平行四边形
是平行四边形![]() 所在平面外一点,如果
所在平面外一点,如果![]() ,
,![]() ,
,![]() .(1)求证:
.(1)求证:![]() 是平面
是平面![]() 的法向量;
的法向量;
(2)求平行四边形![]() 的面积.
的面积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:
(1)由题意结合空间向量数量积的运算法则计算可得![]() ,
,![]() .则
.则![]() ,
,![]() ,结合线面垂直的判断定理可得
,结合线面垂直的判断定理可得![]() 平面
平面![]() ,即
,即![]() 是平面
是平面![]() 的法向量.
的法向量.
(2)利用平面向量的坐标计算可得![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
试题解析:
(1)∵![]() ,
,
![]() .
.
∴![]() ,
,![]() ,又
,又![]() ,∴
,∴![]() 平面
平面![]() ,
,
∴![]() 是平面
是平面![]() 的法向量.
的法向量.
(2)∵![]()
![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
故![]() ,
,![]()
![]() .
.
【题型】解答题
【结束】
19
【题目】(1)求圆心在直线![]() 上,且与直线
上,且与直线![]() 相切于点
相切于点![]() 的圆的方程;
的圆的方程;
(2)求与圆![]() 外切于点
外切于点![]() 且半径为
且半径为![]() 的圆的方程.
的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了确保神舟飞船发射时的信息安全,信息须加密传输,发送方由明文→密文(加密),接受方由密文→明文(解密),已知加密的方法是:密码把英文的明文(真实文)按字母分解,其中英文的a,b,c,…,z的26个字母(不论大小写)依次对应1,2,3,…,26这26个自然数(见下表):
a | b | c | d | e | f | g | h | i | j | k | l | m |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
n | o | p | q | r | s | t | u | v | w | x | y | z |
14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
通过变换公式: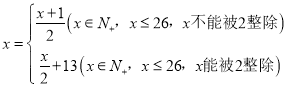 ,将明文转换成密文,如
,将明文转换成密文,如![]() ,即h变换成q;
,即h变换成q;![]() ,即e变换成c.若按上述规定,若将明文译成的密文是shxc,那么原来的明文是__________.
,即e变换成c.若按上述规定,若将明文译成的密文是shxc,那么原来的明文是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018河南濮阳市高三一模】已知点![]() 在抛物线
在抛物线![]() 上,
上, ![]() 是抛物线上异于
是抛物线上异于![]() 的两点,以
的两点,以![]() 为直径的圆过点
为直径的圆过点![]() .
.
(I)证明:直线![]() 过定点;
过定点;
(II)过点![]() 作直线
作直线![]() 的垂线,求垂足
的垂线,求垂足![]() 的轨迹方程.
的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂拟生产甲、乙两种适销产品,每件销售收入分别为3000元,2000元.甲、乙产品都需要在A、B两种设备上加工,在每台A、B设备上加工一件甲所需工时分别为1![]() ,2
,2![]() ,加工一件乙设备所需工时分别为2
,加工一件乙设备所需工时分别为2![]() ,1
,1![]() .A、B两种设备每月有效使用台时数分别为400
.A、B两种设备每月有效使用台时数分别为400![]() 和500
和500![]() ,分别用
,分别用![]() 表示计划每月生产甲,乙产品的件数.
表示计划每月生产甲,乙产品的件数.
(Ⅰ)用![]() 列出满足生产条件的数学关系式,并画出相应的平面区域;
列出满足生产条件的数学关系式,并画出相应的平面区域;
(Ⅱ)问分别生产甲、乙两种产品各多少件,可使收入最大?并求出最大收入.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直线![]() 的参数方程是
的参数方程是 (
(![]() 是参数),圆
是参数),圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求圆心![]() 的直角坐标;
的直角坐标;
(Ⅱ)由直线![]() 上的点向圆
上的点向圆![]() 引切线,求切线长的最小值.
引切线,求切线长的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(1)已知![]() 的解集为
的解集为![]() ,求实数
,求实数![]() 的值;
的值;
(2)已知![]() ,设
,设![]() 、
、![]() 是关于
是关于![]() 的方程
的方程![]() 的两根,且
的两根,且![]() ,求实数
,求实数![]() 的值;
的值;
(3)已知![]() 满足
满足![]() ,且关于
,且关于![]() 的方程
的方程![]() 的两实数根分别在区间
的两实数根分别在区间![]() 内,求实数
内,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com