
【题目】已知点![]() 是平行四边形
是平行四边形![]() 所在平面外一点,如果
所在平面外一点,如果![]() ,
,![]() ,
,![]() .(1)求证:
.(1)求证:![]() 是平面
是平面![]() 的法向量;
的法向量;
(2)求平行四边形![]() 的面积.
的面积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:
(1)由题意结合空间向量数量积的运算法则计算可得![]() ,
,![]() .则
.则![]() ,
,![]() ,结合线面垂直的判断定理可得
,结合线面垂直的判断定理可得![]() 平面
平面![]() ,即
,即![]() 是平面
是平面![]() 的法向量.
的法向量.
(2)利用平面向量的坐标计算可得![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
试题解析:
(1)∵![]() ,
,
![]() .
.
∴![]() ,
,![]() ,又
,又![]() ,∴
,∴![]() 平面
平面![]() ,
,
∴![]() 是平面
是平面![]() 的法向量.
的法向量.
(2)∵![]()
![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
故![]() ,
,![]()
![]() .
.
【题型】解答题
【结束】
19
【题目】(1)求圆心在直线![]() 上,且与直线
上,且与直线![]() 相切于点
相切于点![]() 的圆的方程;
的圆的方程;
(2)求与圆![]() 外切于点
外切于点![]() 且半径为
且半径为![]() 的圆的方程.
的圆的方程.
科目:高中数学 来源: 题型:
【题目】甲、乙、丙、丁四位同学参加比赛,只有其中三位获奖.甲说:“乙或丙未获奖”;乙说:“甲、丙都获奖”;丙说:“我未获奖”;丁说:“乙获奖”.四位同学的话恰有两句是对的,则( )
A. 甲和乙不可能同时获奖 B. 丙和丁不可能同时获奖
C. 乙和丁不可能同时获奖 D. 丁和甲不可能同时获奖
【答案】C
【解析】若甲乙丙同时获奖,则甲丙的话错,乙丁的话对;符合题意;
若甲乙丁同时获奖,则乙的话错,甲丙丁的话对;不合题意;
若甲丙丁同时获奖,则丙丁的话错,甲乙的话对;符合题意;;
若丙乙丁同时获奖,则甲乙丙的话错,丁的话对;不合题意;
因此乙和丁不可能同时获奖,选C.
【题型】单选题
【结束】
12
【题目】已知当![]() 时,关于
时,关于![]() 的方程
的方程![]() 有唯一实数解,则
有唯一实数解,则![]() 值所在的范围是( )
值所在的范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为研究学生的身体素质与与课外体育锻炼时间的关系,对该校200名高三学生的课外体育锻炼平均每天运动的时间进行调查,如下表:(平均每天锻炼的时间单位:分钟)
将学生日均课外体育运动时间在![]() 上的学生评价为“课外体育达标”.
上的学生评价为“课外体育达标”.
平均每天锻炼的时间(分钟) |
|
|
|
|
|
|
总人数 | 20 | 36 | 44 | 50 | 40 | 10 |
请根据上述表格中的统计数据填写下面![]() 列联表,并通过计算判断是否能在犯错误的概率不超过
列联表,并通过计算判断是否能在犯错误的概率不超过![]() 的前提下认为“课外体育达标”与性别有关?
的前提下认为“课外体育达标”与性别有关?
课外体育不达标 | 课外体育达标 | 合计 | |
男 | |||
女 | 20 | 110 | |
合计 |
从上述200名学生中,按“课外体育达标”、“课外体育不达标”分层抽样,抽取4人得到一个样本,再从这个样本中抽取2人,求恰好抽到一名“课外体育不达标”学生的概率.
参考公式:![]() ,其中
,其中![]() .
.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某镇在政府“精准扶贫”的政策指引下,充分利用自身资源,大力发展养殖业,以增加收入,政府计划共投入72万元,全部用于甲、乙两个合作社,每个合作社至少要投入15万元,其中甲合作社养鱼,乙合作社养鸡,在对市场进行调研分析发现养鱼的收益M、养鸡的收益N与投入a(单位:万元)满足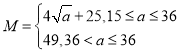 ,N=
,N=![]() a+20.设甲合作社的投入为x(单位:万元),两个合作社的总收益为f(x)(单位:万元).
a+20.设甲合作社的投入为x(单位:万元),两个合作社的总收益为f(x)(单位:万元).
(1)当甲合作社的投入为25万元时,求两个合作社的总收益;
(2)试问如何安排甲、乙两个合作社的投入,才能使总收益最大,最大总收益为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)求圆心在直线![]() 上,且与直线
上,且与直线![]() 相切于点
相切于点![]() 的圆的方程;
的圆的方程;
(2)求与圆![]() 外切于点
外切于点![]() 且半径为
且半径为![]() 的圆的方程.
的圆的方程.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:
(1)由题意可得圆的一条直径所在的直线方程为![]() ,据此可得圆心
,据此可得圆心![]() ,半径
,半径![]() ,则所求圆的方程为
,则所求圆的方程为![]() .
.
(2)圆的标准方程为![]() ,得该圆圆心为
,得该圆圆心为![]() ,半径为
,半径为![]() ,两圆连心线斜率
,两圆连心线斜率![]() .设所求圆心为
.设所求圆心为![]() ,结合弦长公式可得
,结合弦长公式可得![]() ,
,![]() .则圆的方程为
.则圆的方程为![]() .
.
试题解析:
(1)过点![]() 且与直线
且与直线![]() 垂直的直线为
垂直的直线为![]() ,
,
由![]()
![]() .
.
即圆心![]() ,半径
,半径![]() ,
,
所求圆的方程为![]() .
.
(2)圆方程化为![]() ,得该圆圆心为
,得该圆圆心为![]() ,半径为
,半径为![]() ,故两圆连心线斜率
,故两圆连心线斜率![]() .设所求圆心为
.设所求圆心为![]() ,
,
![]() ,∴
,∴![]() ,
,
![]() ,∴
,∴![]() .
.
∴![]() .
.
点睛:求圆的方程,主要有两种方法:
(1)几何法:具体过程中要用到初中有关圆的一些常用性质和定理.如:①圆心在过切点且与切线垂直的直线上;②圆心在任意弦的中垂线上;③两圆相切时,切点与两圆心三点共线.
(2)待定系数法:根据条件设出圆的方程,再由题目给出的条件,列出等式,求出相关量.一般地,与圆心和半径有关,选择标准式,否则,选择一般式.不论是哪种形式,都要确定三个独立参数,所以应该有三个独立等式.
【题型】解答题
【结束】
20
【题目】如图所示,![]() 平面
平面![]() ,点
,点![]() 在以
在以![]() 为直径的
为直径的![]() 上,
上,![]() ,
,![]() ,点
,点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 在弧
在弧![]() 上,且
上,且![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)设二面角![]() 的大小为
的大小为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为实常数).
为实常数).
(1)若![]() ,写出
,写出![]() 的单调递增区间(直接写结果)
的单调递增区间(直接写结果)
(2)若![]() ,设
,设![]() 在区间
在区间![]() 的最小值为
的最小值为![]() ,求
,求![]() 的表达式;
的表达式;
(3)设![]() ,若函数
,若函数![]() 在区间
在区间![]() 上是增函数,求实数
上是增函数,求实数![]() 的取值范围.
的取值范围.
参考结论:函数![]() (
(![]() 为常数),
为常数),![]() 时,
时,![]() 在
在![]() 上递增;
上递增;![]() 时,
时,![]() 在
在![]() 上递减,
上递减,![]() 上递增.
上递增.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医药研究所开发的一种新药,如果成年人按规定的剂量服用,据监测:服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线.

(1)写出第一次服药后,y与t之间的函数关系式y=f(t);
(2)据进一步测定:每毫升血液中含药量不少于0.25微克时,治疗有效.求服药一次后治疗有效的时间是多长?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com