
知{an}是首项为-2的等比数列,Sn是其前n项和,且S3,S2,S4成等差数列,
(1)求数列{an}的通项公式.
(2)若bn=log2|an|,求数列{ }的前n项和Tn.
}的前n项和Tn.
(1) an=(-2)n (2) Tn=1- =
=
【解析】(1)设数列{an}的公比为q,其首项a1=-2.
方法一:①若q=1,则Sn=na1=-2n,
此时S3=-6,S2=-4,S4=-8,S3,S2,S4不成等差数列,不合题意;
②若q≠1,则Sn=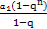 =-
=-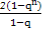
因为S3,S2,S4成等差数列,
所以2S2=S3+S4,即- =-
=-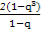 -
-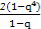 ,
,
整理得q2+q-2=0,
解得q=-2或q=1(舍去),
综上所述,数列{an}的通项公式为an=a1qn-1
=(-2)×(-2)n-1=(-2)n.
方法二:S2=a1+a1q,S3=a1+a1q+a1q2,S4=a1+a1q+a1q2+a1q3.
因为S3,S2,S4成等差数列,
所以2S2=S3+S4,即2a1+2a1q=2a1+2a1q+2a1q2+a1q3,整理得2a1q2+a1q3=0.
因为a1≠0,q≠0,所以q=-2,
故数列{an}的通项公式为an=a1qn-1=(-2)×(-2)n-1=(-2)n.
(2)由(1)可知an=(-2)n,
依题意bn=log2|an|=log2|(-2)n|=log22n=n,
所以 =
= =
=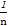 -
- ,
,
所以Tn=(1-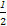 )+(
)+(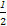 -
-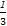 )+…+(
)+…+(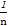 -
- )=1-
)=1- =
= .
.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十六第六章第二节练习卷(解析版) 题型:选择题
“不等式x2-x+m>0在R上恒成立”的一个必要不充分条件是( )
(A)m> (B)0<m<1
(B)0<m<1
(C)m>0 (D)m>1
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十二第五章第三节练习卷(解析版) 题型:解答题
已知{an}是各项均为正数的等比数列,且a1+a2=2( +
+ ),a3+a4+a5=64(
),a3+a4+a5=64( +
+ +
+ ),
),
(1)求{an}的通项公式.
(2)设bn=(an+ )2,求数列{bn}的前n项和Tn.
)2,求数列{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十九第六章第五节练习卷(解析版) 题型:填空题
设等差数列{an}的前n项和为Sn,则S4,S8-S4,S12-S8,S16-S12成等差数列,类比以上结论有:设等比数列{bn}的前n项积为Tn,则T4, , ,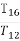 成等比数列.
成等比数列.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十九第六章第五节练习卷(解析版) 题型:选择题
三段论:“①所有的中国人都坚强不屈;②玉树人是中国人;③玉树人一定坚强不屈”中,其中“大前提”和“小前提”分别是( )
(A)①② (B)①③
(C)②③ (D)②①
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十三第五章第四节练习卷(解析版) 题型:填空题
在数列{an}中,若对任意的n均有an+an+1+an+2为定值(n∈N*),且a7=2,a9=3,a98=4,则此数列{an}的前100项的和S100= .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十三第五章第四节练习卷(解析版) 题型:选择题
已知等差数列{an}的公差d≠0,且a1,a3,a9成等比数列,则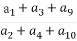 =( )
=( )
(A)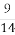 (B)
(B)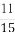 (C)
(C)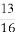 (D)
(D)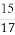
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十七第六章第三节练习卷(解析版) 题型:选择题
若不等式组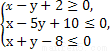 所表示的平面区域被直线y=kx+2分为面积相等的两部分,则k的值为( )
所表示的平面区域被直线y=kx+2分为面积相等的两部分,则k的值为( )
(A) (B)
(B) (C)
(C) (D)2
(D)2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com