
【题目】如图,在四棱锥![]() 中,
中, ![]() 是正方形,
是正方形, ![]() 平面
平面![]() .
. ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别是
分别是 ![]() ,
, ![]() ,
, ![]() 的中点.
的中点.
(1)求证:平面![]() 平面
平面![]() .
.
(2)在线段![]() 上确定一点
上确定一点![]() ,使
,使![]() 平面
平面![]() ,并给出证明.
,并给出证明.

 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:高中数学 来源: 题型:
【题目】小明计划在8月11日至8月20日期间游览某主题公园,根据旅游局统计数据,该主題公园在此期间“游览舒适度”(即在园人数与景区主管部门核定的最大瞬时容量之比, ![]() 以下为舒适,
以下为舒适, ![]() 为一般,
为一般, ![]() 以上为拥挤),情况如图所示,小明随机选择8月11日至8月19日中的某一天到达该主题公园,并游览
以上为拥挤),情况如图所示,小明随机选择8月11日至8月19日中的某一天到达该主题公园,并游览![]() 天.
天.
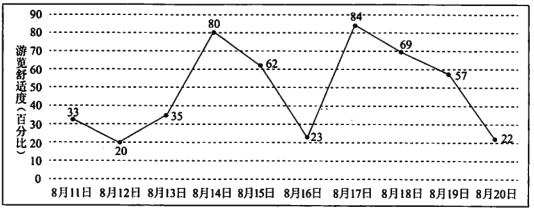
(1)求小明连续两天都遇上拥挤的概率;
(2)设![]() 是小明游览期间遇上舒适的天数,求
是小明游览期间遇上舒适的天数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)由图判断从哪天开始连续三天游览舒适度的方差最大?(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和Sn满足:Sn=n2 , 等比数列{bn}满足:b2=2,b5=16
(1)求数列{an},{bn}的通项公式;
(2)求数列{anbn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中石化集团获得了某地深海油田块的开采权,集团在该地区随机初步勘探了部分几口井,取得了地质资料,进入全面勘探时期后,集团按网络点米布置井位进行全面勘探,由于勘探一口井的费用很高,如果新设计的井位与原有井位重合或接近,便利用旧井的地质资料,不必打这口断井,以节约勘探费用,勘探初期数据资料见下表:
井号 |
|
|
|
|
|
|
坐标 |
|
|
|
|
|
|
钻探深度 |
|
|
|
|
|
|
出油量 |
|
|
|
|
|
|
(1)![]() ~
~![]() 号旧井位置线性分布,借助前5组数据求得回归直线方程为
号旧井位置线性分布,借助前5组数据求得回归直线方程为![]() ,求
,求![]() ,并估计
,并估计![]() 的预报值;
的预报值;
(2)现准备勘探新井![]() ,若通过
,若通过![]() 号并计算出的
号并计算出的![]() 的值(
的值(![]() 精确到
精确到![]() )与(1)中
)与(1)中![]() 的值差不超过
的值差不超过![]() ,则使用位置最接近的已有旧井
,则使用位置最接近的已有旧井![]() ,否则在新位置打开,请判断可否使用旧井?
,否则在新位置打开,请判断可否使用旧井?
(参考公式和计算结果: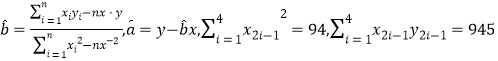 )
)
(3)设出油量与勘探深度的比值![]() 不低于20的勘探井称为优质井,那么在原有
不低于20的勘探井称为优质井,那么在原有![]() 口井中任意勘探
口井中任意勘探![]() 口井,求勘探优质井数
口井,求勘探优质井数![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面内的动点P到定直线l:x=![]() 的距离与点P到定点F(
的距离与点P到定点F(![]() ,0)之比为
,0)之比为![]() .
.
(1)求动点P的轨迹C的方程;
(2)若点N为轨迹C上任意一点(不在x轴上),过原点O作直线AB,交(1)中轨迹C于点A、B,且直线AN、BN的斜率都存在,分别为k1、k2,问k1·k2是否为定值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司即将推车一款新型智能手机,为了更好地对产品进行宣传,需预估市民购买该款手机是否与年龄有关,现随机抽取了50名市民进行购买意愿的问卷调查,若得分低于60分,说明购买意愿弱;若得分不低于60分,说明购买意愿强,调查结果用茎叶图表示如图所示.

(1)根据茎叶图中的数据完成![]() 列联表,并判断是否有95%的把握认为市民是否购买该款手机与年龄有关?
列联表,并判断是否有95%的把握认为市民是否购买该款手机与年龄有关?
购买意愿强 | 购买意愿弱 | 合计 | |
20~40岁 | |||
大于40岁 | |||
合计 |
(2)从购买意愿弱的市民中按年龄进行分层抽样,共抽取5人,从这5人中随机抽取2人进行采访,求这2人都是年龄大于40岁的概率.
附:![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某居民区随机抽取10个家庭,获得第i个家庭的月收入xi(单位:千元)与月储蓄yi(单位:千元)的数据资料,算得 ![]() =80,
=80, ![]() =20,
=20, ![]() yi=184,
yi=184, ![]() =720.
=720.
(1)求家庭的月储蓄y对月收入x的线性回归方程y=bx+a;
(2)判断变量x与y之间是正相关还是负相关;
(3)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
附:线性回归方程y=bx+a中,b= 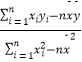 ,a=
,a= ![]() ﹣b
﹣b ![]() ,其中
,其中 ![]() ,
, ![]() 为样本平均值.
为样本平均值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com