
【题目】设数列{an}的前n项和Sn满足:Sn=n2 , 等比数列{bn}满足:b2=2,b5=16
(1)求数列{an},{bn}的通项公式;
(2)求数列{anbn}的前n项和Tn .
【答案】
(1)解: {an}的前n项和Sn满足:Sn=n2,
n=1时,a1=S1=1,n>1时,an=Sn﹣Sn﹣1=n2﹣(n﹣1)2=2n﹣1,
n=1也成立.
故an=2n﹣1,
等比数列{bn}满足:b2=2,b5=16,
q3= ![]() =8,解得q=2.
=8,解得q=2.
则有bn=b2qn﹣2=2n﹣1
(2)解:前n项和Tn=11+32+54+78+…+(2n﹣1)2n﹣1,
2Tn=12+34+58+716+…+(2n﹣1)2n,
两式相减.得﹣Tn=1+22+24+28+216+…+22n﹣1﹣(2n﹣1)2n,
即有﹣Tn=1+ ![]() ﹣(2n﹣1)2n,
﹣(2n﹣1)2n,
则有 ![]() .
.
【解析】(1)由数列的通项和前n项和的关系,可得an的通项,由等比数列的通项可得;(2)由错位相减法,可得数列{anbn}的前n项和Tn .
【考点精析】根据题目的已知条件,利用数列的前n项和和数列的通项公式的相关知识可以得到问题的答案,需要掌握数列{an}的前n项和sn与通项an的关系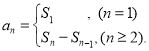 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.


科目:高中数学 来源: 题型:
【题目】设函数f(x)=-![]() x3+x2+(m2-1)x(x∈R),其中m>0.
x3+x2+(m2-1)x(x∈R),其中m>0.
(1)当m=1时,求曲线y=f(x)在点(1,f(1))处的切线斜率;
(2)求函数的单调区间与极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】医学上某种还没有完全攻克的疾病,治疗时需要通过药物控制其中的两项指标![]() 和
和![]() .现有
.现有![]() 三种不同配方的药剂,根据分析,
三种不同配方的药剂,根据分析,![]() 三种药剂能控制
三种药剂能控制![]() 指标的概率分别为0.5,0.6,0.75,能控制
指标的概率分别为0.5,0.6,0.75,能控制![]() 指标的概率分别是0.6,0.5,0.4,能否控制
指标的概率分别是0.6,0.5,0.4,能否控制![]() 指标与能否控制
指标与能否控制![]() 指标之间相互没有影响.
指标之间相互没有影响.
(Ⅰ)求![]() 三种药剂中恰有一种能控制
三种药剂中恰有一种能控制![]() 指标的概率;
指标的概率;
(Ⅱ)某种药剂能使两项指标![]() 和
和![]() 都得到控制就说该药剂有治疗效果.求三种药剂中有治疗效果的药剂种数
都得到控制就说该药剂有治疗效果.求三种药剂中有治疗效果的药剂种数![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把正整数排成如图(a)的三角形阵,然后擦去第偶数行中的所有奇数,第奇数行中的所有偶数,可得如图(b)三角形阵,现将图(b)中的正整数按从小到大的顺序构成一个数列{an},若ak=2017,则k= . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中, ![]() 是正方形,
是正方形, ![]() 平面
平面![]() .
. ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别是
分别是 ![]() ,
, ![]() ,
, ![]() 的中点.
的中点.
(1)求证:平面![]() 平面
平面![]() .
.
(2)在线段![]() 上确定一点
上确定一点![]() ,使
,使![]() 平面
平面![]() ,并给出证明.
,并给出证明.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】微信是现代生活中进行信息交流的重要工具.据统计,某公司200名员工中90%的人使用微信,其中每天使用微信时间在一小时以内的有60人,其余的员工每天使用微信时间在一小时以上,若将员工分成青年(年龄小于40岁)和中年(年龄不小于40岁)两个阶段,那么使用微信的人中75%是青年人.若规定:每天使用微信时间在一小时以上为经常使用微信,那么经常使用微信的员工中都是青年人.
(1)若要调查该公司使用微信的员工经常使用微信与年龄的关系,列出并完成2×2列联表:

(2)由列联表中所得数据判断,是否有99.9%的把握认为“经常使用微信与年龄有关”?
(3)采用分层抽样的方法从“经常使用微信”的人中抽取6人,从这6人中任选2人,求选出的2人,均是青年人的概率.
附:

![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() 与动直线
与动直线![]() 的交点为
的交点为![]() ,线段
,线段![]() 的中垂线与动直线
的中垂线与动直线![]() 的交点为
的交点为![]() .
.

(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过动点![]() 作曲线
作曲线![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,
,![]() ,求证:
,求证:![]() 的大小为定值.
的大小为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com