
【题目】如图,在直三棱柱![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 是
是![]() 的中点.
的中点.

①求证: ![]() .
.
②求点![]() 到平面
到平面![]() 的距离.
的距离.
③求二面角![]() 的余弦值的大小.
的余弦值的大小.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】试题分析:(1)由等腰三角形得![]() ,由
,由![]() 平面
平面![]() 得
得![]() ,故而可得
,故而可得![]() 平面
平面![]() ,最后得结论;(2)点
,最后得结论;(2)点![]() 到平面
到平面![]() 的距离为
的距离为![]() .通过
.通过![]() 转化
转化![]() ,求点
,求点![]() 到平面
到平面![]() 的距离;(3)以
的距离;(3)以![]() 为坐标原点,
为坐标原点, ![]() ,
, ![]() ,
, ![]() 为
为![]() ,
, ![]() ,
, ![]() 轴,建立空间直角坐标系,求出面
轴,建立空间直角坐标系,求出面![]() 和面
和面![]() 的法向量,计算法向量的夹角,根据图可判断二面角为锐角,故可得角的大小.
的法向量,计算法向量的夹角,根据图可判断二面角为锐角,故可得角的大小.
试题解析:(1)∵在等腰![]() 中,
中, ![]() 为斜边
为斜边![]() 中点,∴
中点,∴![]() ,又∵在直三棱柱
,又∵在直三棱柱![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴ ![]() ,∵
,∵![]() 点,
点, ![]() 、
、![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() .
.
(2)设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,在三棱锥
,在三棱锥![]() 中,∵
中,∵![]() ,且
,且![]() 平面
平面![]() ,∴
,∴![]() ,易求得
,易求得![]() ,
, ![]() ,∴
,∴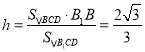 ,即点
,即点![]() 到平面
到平面![]() 的距离是
的距离是![]()
(3)如图,
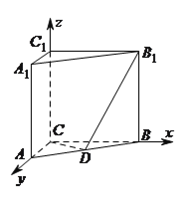
以![]() 为坐标原点,
为坐标原点, ![]() ,
, ![]() ,
, ![]() 为
为![]() ,
, ![]() ,
, ![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .设平面
.设平面![]() 的一个法向量
的一个法向量![]() ,
, ![]() ,
, ![]() ,设平面
,设平面![]() 的一个法向量
的一个法向量![]() ,
, ![]() ,
, ![]() ,∴
,∴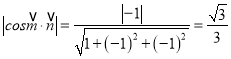 ,由图知,所求二面角为锐角,余弦值为
,由图知,所求二面角为锐角,余弦值为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 为菱形,
为菱形, ![]() ,
, ![]() 与
与![]() 相交于点
相交于点![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() 为
为![]() 中点.
中点.
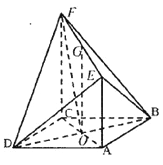
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的正弦值;
的正弦值;
(Ⅲ)当直线![]() 与平面
与平面![]() 所成角为
所成角为![]() 时,求异面直线
时,求异面直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明计划在8月11日至8月20日期间游览某主题公园,根据旅游局统计数据,该主題公园在此期间“游览舒适度”(即在园人数与景区主管部门核定的最大瞬时容量之比, ![]() 以下为舒适,
以下为舒适, ![]() 为一般,
为一般, ![]() 以上为拥挤),情况如图所示,小明随机选择8月11日至8月19日中的某一天到达该主题公园,并游览
以上为拥挤),情况如图所示,小明随机选择8月11日至8月19日中的某一天到达该主题公园,并游览![]() 天.
天.
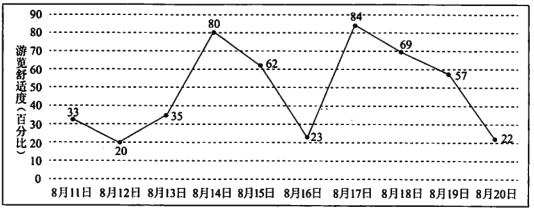
(1)求小明连续两天都遇上拥挤的概率;
(2)设![]() 是小明游览期间遇上舒适的天数,求
是小明游览期间遇上舒适的天数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)由图判断从哪天开始连续三天游览舒适度的方差最大?(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在正方形![]() 中,点
中,点![]() 分别是
分别是![]() 的中点,
的中点,![]() 与
与![]() 交于点
交于点![]() ,点
,点![]() 分别在线段
分别在线段![]() 上,且
上,且![]() .将
.将![]() 分别沿
分别沿![]() 折起,使点
折起,使点![]() 重合于点
重合于点![]() ,如图2所示.
,如图2所示.
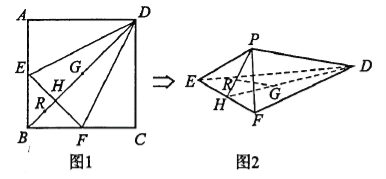
(1)求证:![]() 平面
平面![]() ;
;
(2)若正方形![]() 的边长为4,求三棱锥
的边长为4,求三棱锥![]() 的内切球的半径.
的内切球的半径.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和Sn满足:Sn=n2 , 等比数列{bn}满足:b2=2,b5=16
(1)求数列{an},{bn}的通项公式;
(2)求数列{anbn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中石化集团获得了某地深海油田块的开采权,集团在该地区随机初步勘探了部分几口井,取得了地质资料,进入全面勘探时期后,集团按网络点米布置井位进行全面勘探,由于勘探一口井的费用很高,如果新设计的井位与原有井位重合或接近,便利用旧井的地质资料,不必打这口断井,以节约勘探费用,勘探初期数据资料见下表:
井号 |
|
|
|
|
|
|
坐标 |
|
|
|
|
|
|
钻探深度 |
|
|
|
|
|
|
出油量 |
|
|
|
|
|
|
(1)![]() ~
~![]() 号旧井位置线性分布,借助前5组数据求得回归直线方程为
号旧井位置线性分布,借助前5组数据求得回归直线方程为![]() ,求
,求![]() ,并估计
,并估计![]() 的预报值;
的预报值;
(2)现准备勘探新井![]() ,若通过
,若通过![]() 号并计算出的
号并计算出的![]() 的值(
的值(![]() 精确到
精确到![]() )与(1)中
)与(1)中![]() 的值差不超过
的值差不超过![]() ,则使用位置最接近的已有旧井
,则使用位置最接近的已有旧井![]() ,否则在新位置打开,请判断可否使用旧井?
,否则在新位置打开,请判断可否使用旧井?
(参考公式和计算结果: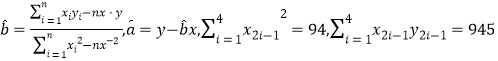 )
)
(3)设出油量与勘探深度的比值![]() 不低于20的勘探井称为优质井,那么在原有
不低于20的勘探井称为优质井,那么在原有![]() 口井中任意勘探
口井中任意勘探![]() 口井,求勘探优质井数
口井,求勘探优质井数![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司即将推车一款新型智能手机,为了更好地对产品进行宣传,需预估市民购买该款手机是否与年龄有关,现随机抽取了50名市民进行购买意愿的问卷调查,若得分低于60分,说明购买意愿弱;若得分不低于60分,说明购买意愿强,调查结果用茎叶图表示如图所示.

(1)根据茎叶图中的数据完成![]() 列联表,并判断是否有95%的把握认为市民是否购买该款手机与年龄有关?
列联表,并判断是否有95%的把握认为市民是否购买该款手机与年龄有关?
购买意愿强 | 购买意愿弱 | 合计 | |
20~40岁 | |||
大于40岁 | |||
合计 |
(2)从购买意愿弱的市民中按年龄进行分层抽样,共抽取5人,从这5人中随机抽取2人进行采访,求这2人都是年龄大于40岁的概率.
附:![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列{an}的前n项和为Sn , 且an和Sn满足:4Sn=(an+1)2(n=1,2,3…),
(1)求{an}的通项公式;
(2)设bn= ![]() ,求{bn}的前n项和Tn .
,求{bn}的前n项和Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com