Question

【题目】已知正项数列{an}的前n项和为Sn ， 且an和Sn满足：4Sn=（an+1）2（n=1，2，3…），
（1）求{an}的通项公式；
（2）设bn= ，求{bn}的前n项和Tn ．

Answer 1

【答案】
（1）解：∵4Sn=（an+1）2，①

∴4Sn﹣1=（an﹣1+1）2（n≥2），②

①﹣②得

4（Sn﹣Sn﹣1）=（an+1）2﹣（an﹣1+1）2．

∴4an=（an+1）2﹣（an﹣1+1）2．

化简得（an+an﹣1）（an﹣an﹣1﹣2）=0．

∵an＞0，∴an﹣an﹣1=2（n≥2）．

∴{an}是以1为首项，2为公差的等差数列．

∴an=1+（n﹣1）2=2n﹣1

（2）解：bn= = = （ ﹣ ）．

∴Tn= +…+

= （1﹣ ）=

【解析】（1）利用递推关系、等差数列的通项公式即可得出；（2）利用“裂项求和”方法即可得出．
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识，掌握数列{an}的前n项和sn与通项an的关系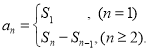，以及对数列的通项公式的理解，了解如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式．