
【题目】甲乙两人下棋比赛,规定谁比对方先多胜两局谁就获胜,比赛立即结束;若比赛进行完6局还没有分出胜负则判第一局获胜者为最终获胜且结束比赛.比赛过程中,每局比赛甲获胜的概率为![]() ,乙获胜的概率为
,乙获胜的概率为![]() ,每局比赛相互独立.求:(1)比赛两局就结束且甲获胜的概率;(2)恰好比赛四局结束的概率;(3)在整个比赛过程中,甲获胜的概率.
,每局比赛相互独立.求:(1)比赛两局就结束且甲获胜的概率;(2)恰好比赛四局结束的概率;(3)在整个比赛过程中,甲获胜的概率.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)根据独立事件同时发生的概率公式求解;(2)前两局甲乙各胜一局,最后两局甲胜或最后两局乙胜分两种情况求概率和即可;(3)求出各种情况下甲获胜的概率,然后求和即可.
试题解析:(1)由题意可知比赛两局就结束且甲获胜必须第一、第二局比赛都是甲获胜,概率为![]() ;(2)由题意知前两局比赛为平手,第三、第四局比赛为同一个人胜,其概率为
;(2)由题意知前两局比赛为平手,第三、第四局比赛为同一个人胜,其概率为![]() ;(3)由题意知在整个比赛过程中第一、第二局比赛两人为平手,第三、第四比赛两人也为平手,第五、第六局都为甲获胜,或者在第一、第二局比赛两人为平手,第三、第四局比赛两人也为平手,第五、第六局比赛为平手但第一局是甲获胜.其概率为
;(3)由题意知在整个比赛过程中第一、第二局比赛两人为平手,第三、第四比赛两人也为平手,第五、第六局都为甲获胜,或者在第一、第二局比赛两人为平手,第三、第四局比赛两人也为平手,第五、第六局比赛为平手但第一局是甲获胜.其概率为![]() .
.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】设函数![]() (
(![]() ,
,![]() ,
,![]() ,
,![]() )的图象在点
)的图象在点![]() 处的切线的斜率为
处的切线的斜率为![]() ,且函数
,且函数![]() 为偶函数.若函数
为偶函数.若函数![]() 满足下列条件:①
满足下列条件:①![]() ;②对一切实数
;②对一切实数![]() ,不等式
,不等式![]() 恒成立.
恒成立.
(1)求函数![]() 的表达式;
的表达式;
(2)设函数![]() (
(![]() )的两个极值点
)的两个极值点![]() ,
,![]() (
(![]() )恰为
)恰为![]() 的零点.当
的零点.当![]() 时,求
时,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海关对同时从![]() ,
,![]() ,
,![]() 三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如下表所示.工作人员用分层抽样的方法从这些商品中共抽取6件样品进行检测.
三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如下表所示.工作人员用分层抽样的方法从这些商品中共抽取6件样品进行检测.
地区 |
|
|
|
数量 | 50 | 150 | 100 |
(1)求这6件样品中来自![]() ,
,![]() ,
,![]() 各地区商品的数量;
各地区商品的数量;
(2)若在这6件样品中随机抽取2件送往甲机构进行进一步检测,求这2件商品来自相同地区的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】水是万物之本、生命之源,节约用水,从我做起.我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准![]() (吨)、一位居民的月用水量不超过
(吨)、一位居民的月用水量不超过![]() 的部分按平价收费,超出
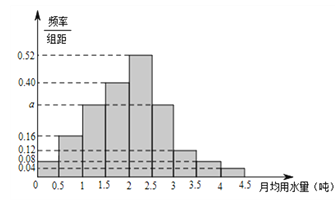
的部分按平价收费,超出![]() 的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.(1)求直方图中a的值;(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;(3)若该市政府希望使85%的居民每月的用水量不超过标准
的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.(1)求直方图中a的值;(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;(3)若该市政府希望使85%的居民每月的用水量不超过标准![]() (吨),估计
(吨),估计![]() 的值,并说明理由.
的值,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,直线
,直线![]() 经过点A (1,0).
经过点A (1,0).
(1)若直线![]() 与圆C相切,求直线
与圆C相切,求直线![]() 的方程;
的方程;
(2)若直线![]() 与圆C相交于P,Q两点,求三角形CPQ面积的最大值,并求此时直线
与圆C相交于P,Q两点,求三角形CPQ面积的最大值,并求此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,
,![]() 为
为![]() 上异于原点的任意一点,过点
上异于原点的任意一点,过点![]() 的直线
的直线![]() 交
交![]() 于另一点
于另一点![]() ,交
,交![]() 轴的正半轴于点
轴的正半轴于点![]() ,且有
,且有![]() .当点
.当点![]() 的横坐标为3时,
的横坐标为3时,![]() 为正三角形.
为正三角形.
(1)求![]() 的方程;
的方程;
(2)延长![]() 交抛物线于点
交抛物线于点![]() ,过点
,过点![]() 作抛物线的切线
作抛物线的切线![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】同时抛掷甲、乙两颗骰子.
(1)求事件A“甲的点数大于乙的点数”的概率;
(2)若以抛掷甲、乙两颗骰子点数m,n作为点P的坐标(m,n),求事件B“P落在圆![]() 内”的概率.
内”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com