
如图,在矩形ABCD中,AB> ·AD,E为AD的中点,连结EC,作EF⊥EC,且EF交AB于F,连结FC.设
·AD,E为AD的中点,连结EC,作EF⊥EC,且EF交AB于F,连结FC.设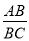 =k,是否存在实数k,使△AEF、△ECF、△DCE与△BCF都相似?若存在,给出证明;若不存在,请说明理由.
=k,是否存在实数k,使△AEF、△ECF、△DCE与△BCF都相似?若存在,给出证明;若不存在,请说明理由.


【解析】假设存在实数k的值,满足题设.
①先证明△AEF∽△DCE∽△ECF.因为EF⊥EC,
所以∠AEF=90°-∠DEC=∠DCE.
而∠A=∠D=90°,故△AEF∽△DCE.
故得 .又DE=EA,所以
.又DE=EA,所以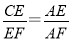 .
.
又∠CEF=∠EAF=90°,所以△AEF∽△ECF.
②再证明可以取到实数k的值,使△AEF∽△BCF,
由于∠AFE+∠BFC≠90°,故不可能有∠AFE=∠BFC,
因此要使△AEF∽△BCF,应有∠AFE=∠BFC,
此时,有 ,又AE=
,又AE=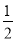 BC,故得AF=
BC,故得AF= BF=
BF= AB.
AB.
由△AEF∽△DCE,可知 ,
,
因此, AB2,所以
AB2,所以 ,求得k=
,求得k= .
.
可以验证,当k= 时,这四个三角形都是有一个锐角等于60°的直角三角形,故它们都相似.
时,这四个三角形都是有一个锐角等于60°的直角三角形,故它们都相似.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨选修4-1第2课时练习卷(解析版) 题型:解答题
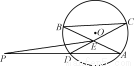
如图,弦AB与CD相交于⊙O内一点E,过E作BC的平行线与AD的延长线相交于点P.已知PD=2DA=2,求PE.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨选修4-1第2课时练习卷(解析版) 题型:解答题
如图,AC为圆O的直径,弦BD⊥AC于点P,PC=2,PA=8,求tan∠ACD的值.

查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨选修4-1第1课时练习卷(解析版) 题型:解答题
如图,梯形ABCD中,AD∥BC,EF是中位线,BD交EF于P,已知EP∶PF=1∶2,AD=7cm,求BC的长.

查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨选修4-1第1课时练习卷(解析版) 题型:解答题
如图,四边形ABCD中,DF⊥AB,垂足为F,DF=3,AF=2FB=2,延长FB到E,使BE=FB.连结BD、EC,若BD∥EC,求△BCD和四边形ABCD的面积.

查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第十章第6课时练习卷(解析版) 题型:填空题
甲、乙二人下棋,甲获胜的概率是0.3,甲不输的概率为0.8,则甲、乙二人下成和棋的概率为________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第十章第5课时练习卷(解析版) 题型:填空题
连续掷两次骰子分别得到点数m、n,则向量(m,n)与向量(-1,1)的夹角θ>90°的概率是________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第十章第3课时练习卷(解析版) 题型:填空题
某班有48名学生,在一次考试中统计出平均分数为70,方差为75,后来发现有2名同学的成绩有误,甲实得80分却记为50分,乙实得70分却记为100分,更正后平均分和方差分别是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com