
已知半径为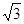 的球内有一个内接正方体(即正方体的顶点都在球面上).
的球内有一个内接正方体(即正方体的顶点都在球面上).
(1)求此球的体积;
(2)求此球的内接正方体的体积;
(3)求此球的表面积与其内接正方体的全面积之比.
(1)V=4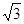
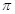 ;(2)V=8;(3)球的表面积与其内接正方体的全面积之比为
;(2)V=8;(3)球的表面积与其内接正方体的全面积之比为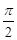 .
.
解析试题分析:(1)球的体积公式为V=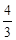
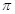 R3,将R=
R3,将R=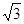 代入可得V=4
代入可得V=4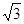
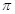 ;(2)要求内接正方体的体积,需要知道正方体的棱长,正方体的对角线是球的直径,而正方体的对角线是棱长的
;(2)要求内接正方体的体积,需要知道正方体的棱长,正方体的对角线是球的直径,而正方体的对角线是棱长的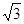 倍,设正方体的棱长为a,所以2
倍,设正方体的棱长为a,所以2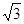 =
=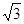 a,a="2," V=a3=8;(3)求出正方体的表面积和球的表面积,从而得出球的球面面积与其内接正方体的全面积之比,S球=4
a,a="2," V=a3=8;(3)求出正方体的表面积和球的表面积,从而得出球的球面面积与其内接正方体的全面积之比,S球=4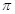 R2=12
R2=12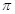 ,S正方体=6a2=24,所以这个球的表面积与其内接正方体的全面积之比为12
,S正方体=6a2=24,所以这个球的表面积与其内接正方体的全面积之比为12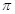 :24=
:24=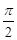 .
.
试题解析:(1)球的体积V=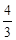
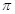 R3=4
R3=4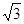
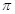 ;
;
(2)设正方体的棱长为a,
∴2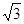 =
=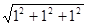 a =
a =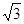 a,a="2," V=a3=8;
a,a="2," V=a3=8;
(3)S球=4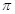 R2=12
R2=12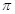 ,
,
S正方体=6a2=24,
∴这个球的表面积与其内接正方体的全面积之比为12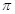 :24=
:24=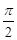 .
.
考点:1.球的体积公式;2.球内接多面体.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
如图1所示,在Rt△ABC中,AC=6,BC=3,∠ABC=90°,CD为∠ACB的平分线,点E在线段AC上,CE=4.如图2所示,将△BCD沿CD折起,使得平面BCD⊥平面ACD,连接AB,设点F是AB的中点.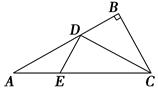
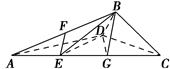
图1 图2
(1)求证:DE⊥平面BCD;
(2)若EF∥平面BDG,其中G为直线AC与平面BDG的交点,求三棱锥BDEG的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在长方体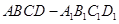 中,
中,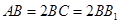 , 沿平面
, 沿平面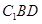 把这个长方体截成两个几何体: 几何体(1);几何体(2)
把这个长方体截成两个几何体: 几何体(1);几何体(2)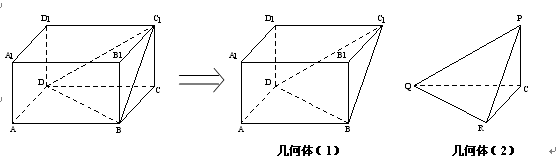
(I)设几何体(1)、几何体(2)的体积分为是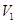 、
、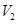 ,求
,求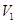 与
与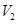 的比值
的比值
(II)在几何体(2)中,求二面角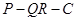 的正切值
的正切值
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,正三棱柱ABC—A1B1C1的各棱长都相等,M、E分别是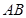 和AB1的中点,点F在BC上且满足BF∶FC=1∶3.
和AB1的中点,点F在BC上且满足BF∶FC=1∶3.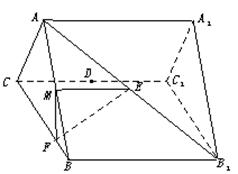
(1)求证:BB1∥平面EFM;
(2)求四面体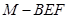 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在三棱柱ABC-A1B1C1中,A1B⊥平面ABC,AB⊥AC.
(1)求证:AC⊥BB1;
(2)若P是棱B1C1的中点,求平面PAB将三棱柱分成的两部分体积之比.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com