
【题目】已知直线的参数方程为![]() (t为参数,α∈[0,π).以O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=ρcosθ+2,
(t为参数,α∈[0,π).以O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=ρcosθ+2,
(1)若![]() ,求直线的极坐标方程
,求直线的极坐标方程
(2)若直线与曲线C有唯一公共点,求α
【答案】(1)![]() .(2)α=0、
.(2)α=0、![]() 或
或![]()
【解析】
(1)当![]() 时,直线l的参数方程为
时,直线l的参数方程为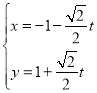 (t为参数),先转化为直角坐标方程,再得到直线l的极坐标方程.
(t为参数),先转化为直角坐标方程,再得到直线l的极坐标方程.
(2)先将曲线C的极坐标方程ρ=ρcosθ+2,化为直角坐标方程y2=4x+4,再将参数方程![]() 代入y2=4x+4,化简得t2sin2α+2t(sinα﹣2cosα)+1=0,然后根据直线l曲线C一公共点,转化为关于t的方程t2sin2α+2t(sinα﹣2cosα)+1=0,α∈[0,π)有唯一解求解.
代入y2=4x+4,化简得t2sin2α+2t(sinα﹣2cosα)+1=0,然后根据直线l曲线C一公共点,转化为关于t的方程t2sin2α+2t(sinα﹣2cosα)+1=0,α∈[0,π)有唯一解求解.
(1)当![]() 时,直线l的参数方程为
时,直线l的参数方程为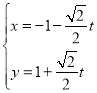 (t为参数),所以直角坐标方程为x+y=0,
(t为参数),所以直角坐标方程为x+y=0,
由于直线经过极点且倾斜角为![]() ,所以直线l的极坐标方程
,所以直线l的极坐标方程![]() .
.
(2)ρ=ρcosθ+2,所以ρ2=(ρcosθ+2)2,
即x2+y2=(x+2)2,即y2=4x+4,
将参数方程![]() 代入y2=4x+4,
代入y2=4x+4,
化简得,t2sin2α+2t(sinα﹣2cosα)+1=0
因为直线l曲线C一个公共点,
所以关于t的方程t2sin2α+2t(sinα﹣2cosα)+1=0,α∈[0,π)有唯一解
①当sin2α=0即α=0时,![]() 符合题意;
符合题意;
②当cosα≠0时,[2(sinα﹣2cosα)]2﹣4sin2α=0,
即cosα(cosα﹣sinα)=0,
所以cosα=0或cosα=sinα,
又α∈[0,π),所以![]() 或
或![]()
综上,直线l与曲线C唯一公共点时,α=0、![]() 或
或![]()


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() (
(![]() ).
).
(1)若曲线![]() 在
在![]() 处的切线也是曲线
处的切线也是曲线![]() 的切线,求
的切线,求![]() 的值;
的值;
(2)记![]() ,设
,设![]() 是函数
是函数![]() 的两个极值点,且
的两个极值点,且![]() .
.
① 若![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
② 判断函数![]() 的零点个数,并说明理由.
的零点个数,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图像向左平移
的图像向左平移![]() 个单位,再将所有点的横坐标缩短到原来的
个单位,再将所有点的横坐标缩短到原来的![]() 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数![]() 的图像则下面对函数
的图像则下面对函数![]() 的叙述不正确的是( )
的叙述不正确的是( )
A.函数![]() 的周期
的周期![]()
B.函数![]() 的一个对称中心
的一个对称中心![]()
C.函数![]() 在区间
在区间![]() 内单调递增
内单调递增
D.当![]() ,
,![]() 时,函数
时,函数![]() 有最小值
有最小值![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:从数列{an}中抽取m(m∈N,m≥3)项按其在{an}中的次序排列形成一个新数列{bn},则称{bn}为{an}的子数列;若{bn}成等差(或等比),则称{bn}为{an}的等差(或等比)子数列.
(1)记数列{an}的前n项和为Sn,已知![]() .
.
①求数列{an}的通项公式;
②数列{an}是否存在等差子数列,若存在,求出等差子数列;若不存在,请说明理由.
(2)已知数列{an}的通项公式为an=n+a(a∈Q+),证明:{an}存在等比子数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中装有9只球,其中标有数字1,2,3,4的小球各2个,标数字5的小球有1个.从袋中任取3个小球,每个小球被取出的可能性都相等,用![]() 表示取出的3个小球上的最大数字.
表示取出的3个小球上的最大数字.
(1)求取出的3个小球上的数字互不相同的概率;
(2)求随机变量![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某篮球队员进行定点投篮训练,每次投中的概率是![]() ,且每次投篮的结果互不影响.
,且每次投篮的结果互不影响.
(1)假设这名队员投篮5次,求恰有2次投中的概率;
(2)假设这名队员投篮3次,每次投篮,投中得1分,为投中得0分,在3次投篮中,若有2次连续投中,而另外一次未投中,则额外加1分;若3次全投中,则额外加3分,记![]() 为队员投篮3次后的总的分数,求
为队员投篮3次后的总的分数,求![]() 的分布列及期望.
的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
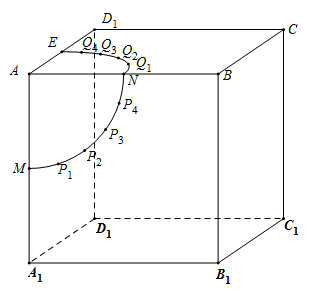
【题目】如图,棱长为2的正方体![]() 中,点
中,点![]() 分别为棱
分别为棱![]() 的中点,以
的中点,以![]() 为圆心,1为半径,分别在面
为圆心,1为半径,分别在面![]() 和面
和面![]() 内作弧
内作弧![]() 和
和![]() ,并将两弧各五等分,分点依次为
,并将两弧各五等分,分点依次为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 以及
以及![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .一只蚂蚁欲从点
.一只蚂蚁欲从点![]() 出发,沿正方体的表面爬行至
出发,沿正方体的表面爬行至![]() ,则其爬行的最短距离为________.参考数据:
,则其爬行的最短距离为________.参考数据:![]() ;
;![]() ;
;![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com