
【题目】已知函数![]() ,
,![]() (
(![]() ).
).
(1)若曲线![]() 在
在![]() 处的切线也是曲线
处的切线也是曲线![]() 的切线,求
的切线,求![]() 的值;
的值;
(2)记![]() ,设
,设![]() 是函数
是函数![]() 的两个极值点,且
的两个极值点,且![]() .
.
① 若![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
② 判断函数![]() 的零点个数,并说明理由.
的零点个数,并说明理由.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②函数
;②函数![]() 有且仅有1个零点,理由见解析
有且仅有1个零点,理由见解析
【解析】
(1)根据导数的几何意义可求得曲线![]() 在
在![]() 处的切线方程,再联立切线与
处的切线方程,再联立切线与![]() ,利用判别式为0解决相切问题即可.
,利用判别式为0解决相切问题即可.
(2) ①易得![]() ,再求导根据韦达定理可知极值点满足
,再求导根据韦达定理可知极值点满足![]() ,再求解化简
,再求解化简![]() ,构造出函数
,构造出函数![]() ,求导分析函数
,求导分析函数![]() 的单调性,进而求得
的单调性,进而求得![]() 的最小值即可.
的最小值即可.
②根据①中![]() 的单调性以及极值点可知
的单调性以及极值点可知![]() ,且
,且![]() ,代入
,代入![]() 分析可知
分析可知![]() ,再根据零点存在性定理判定
,再根据零点存在性定理判定![]() ,使得
,使得![]() 即可知有1个零点.
即可知有1个零点.
(1)当![]() 时,
时,![]() ,又
,又![]() ,所以
,所以![]() ,则曲线
,则曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() .
.
由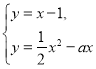 得
得![]() ,因为
,因为![]() 也是曲线
也是曲线![]() 的切线,所以
的切线,所以![]() ,
,
解之得![]() .
.
(2)①因为![]() ,所以
,所以![]() ,
,
由![]() 得
得![]() ,所以
,所以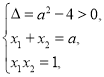 则
则![]() .
.
因为![]() ,所以
,所以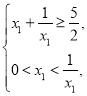 解得
解得![]() .
.
所以![]()
![]()
![]()
![]() .
.
设![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 上单调递减,当
上单调递减,当![]() 时,
时,![]() ,
,
所以![]() ,即所求
,即所求![]() 的取值范围为
的取值范围为![]() .
.
② 由①知当![]() 时,
时,![]() ,
,![]() 单调递增,当
单调递增,当![]() 时,
时,![]() ,
,![]() 单调递减,当
单调递减,当![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
又![]() ,且由①知
,且由①知![]() ,
,
所以![]() ,
,
又![]() ,所以
,所以![]() ,
,![]() ,则
,则![]() ,
,
所以当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
所以当![]() 时,
时,![]() ,则当
,则当![]() 时,
时,![]() 没有零点.
没有零点.
因为![]() ,
,![]() ,
,![]() ,
,
又![]() 在
在![]() 上单调递增,且图像连续不间断,所以
上单调递增,且图像连续不间断,所以![]() ,使得
,使得![]() .
.
综上所述,函数![]() 有且仅有1个零点.
有且仅有1个零点.


科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() ,若圆
,若圆![]()
![]() 的一条切线与椭圆
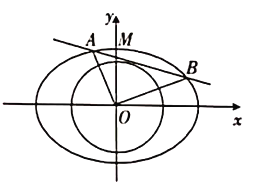
的一条切线与椭圆![]() 有两个交点
有两个交点![]() ,且
,且![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)已知椭圆![]() 的上顶点为
的上顶点为![]() ,点
,点![]() 在圆
在圆![]() 上,直线
上,直线![]() 与椭圆
与椭圆![]() 相交于另一点
相交于另一点![]() ,且
,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知甲、乙、丙三个组的老年人数分别为30,30,24.现用分层抽样的方法从中抽取14人,进行身体状况调查.
(1)应从甲、乙、丙三个小组各抽取多少人?
(2)若抽出的14人中,10人身体状况良好,还有4人有不同程度的状况要进行治疗,现从这14人中,再抽3人进一步了解情况,用![]() 表示抽取的3人中,身体状况良好的人数,求
表示抽取的3人中,身体状况良好的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线的参数方程为![]() (t为参数,α∈[0,π).以O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=ρcosθ+2,
(t为参数,α∈[0,π).以O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=ρcosθ+2,
(1)若![]() ,求直线的极坐标方程
,求直线的极坐标方程
(2)若直线与曲线C有唯一公共点,求α
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com