
【题目】已知函数![]() .
.
(1)当![]() 时,讨论
时,讨论![]() 的单调性;
的单调性;
(2)若不等式![]() 对
对![]() ,
,![]() 恒成立,求正数
恒成立,求正数![]() 的取值范围.
的取值范围.
【答案】(1)见解析(2)![]()
【解析】
(1)求函数的导数,当![]() 时,分类讨论
时,分类讨论![]() 也可求得
也可求得![]() 的单调性;
的单调性;
(2)若不等式![]() 对
对![]() ,
,![]() 恒成立,将原问题等价于对任意的
恒成立,将原问题等价于对任意的![]() ,
,![]() 有
有![]() 成立,设
成立,设![]() ,
,![]() ,
,![]() ,
,![]() ,求函数的最值从而可求正数
,求函数的最值从而可求正数![]() 的取值范围.
的取值范围.
解:函数![]() .
.
所以![]() .
.
(1)①当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
②当![]() 时,
时,![]() ,
,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
![]() ,
,![]() .
.![]() 在
在![]() 上单调递减;
上单调递减;
![]() ,
,![]() ,
,![]() 在
在![]() 上单调递增.
上单调递增.
③当![]() 时,
时,![]() ,
,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
![]() ,
,![]() ,
,![]() 在
在![]() 上单调递减;
上单调递减;
![]() ,
,![]() .
.![]() 在
在![]() 上单调递增;
上单调递增;
(2)若不等式![]() 对
对![]() ,
,![]() 恒成立,
恒成立,
原问题等价于对任意的![]() ,
,![]() 有
有![]() 成立,
成立,
设![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
令![]() ,得:
,得:![]() ;令
;令![]() ,得:
,得:![]() .
.
所以函数![]() 在
在![]() ,
,![]() 上单调递减,在
上单调递减,在![]() ,
,![]() 上单调递增,
上单调递增,
![]() 与
与![]() 中的较大者,
中的较大者,
设![]() ,
,![]()
则![]() ,
,
所以![]() 在
在![]() 上单调递增,故
上单调递增,故![]() ,即
,即![]() ,
,
从而![]() ,故
,故![]() ,即
,即![]() .
.
设![]() ,则有
,则有![]() ,
,
所以![]() 在
在![]() 上单调递增,
上单调递增,
又因为![]() ,
,
所以![]() ,可得:
,可得:![]() ,
,
因为![]() ,所以
,所以![]() 的取值范围为:
的取值范围为:![]() ,
,![]() .
.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为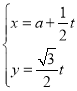 ,以直角坐标系
,以直角坐标系![]() 的
的![]() 点为极点,
点为极点,![]() 为极轴,且取相同的长度单位,建立极坐标系,已知圆
为极轴,且取相同的长度单位,建立极坐标系,已知圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的倾斜角;
的倾斜角;
(2)若直线![]() 与圆
与圆![]() 交于
交于![]() 两点,当
两点,当![]() 的面积最大时,求实数
的面积最大时,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,且
,且![]() ,椭圆经过点
,椭圆经过点![]() .
.
(1)求椭圆的方程;
(2)直线![]() 过椭圆右顶点
过椭圆右顶点![]() ,交椭圆于另一点
,交椭圆于另一点![]() ,点
,点![]() 在直线
在直线![]() 上,且
上,且![]() .若
.若![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
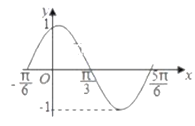
【题目】如图是函数![]() 在区间
在区间![]() 上的图象,为了得到这个函数的图象,只需将
上的图象,为了得到这个函数的图象,只需将![]() 的图象上的所有的点( )
的图象上的所有的点( )
A.向左平移![]() 个长度单位,再把所得各点的横坐标变为原来的
个长度单位,再把所得各点的横坐标变为原来的![]() ,纵坐标不变
,纵坐标不变
B.向左平移![]() 个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变
个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变
C.向左平移![]() 个长度单位,再把所得各点的横坐标变为原来的
个长度单位,再把所得各点的横坐标变为原来的![]() ,纵坐标不变
,纵坐标不变
D.向左平移![]() 个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变
个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() (
(![]() ).
).
(1)若曲线![]() 在
在![]() 处的切线也是曲线
处的切线也是曲线![]() 的切线,求
的切线,求![]() 的值;
的值;
(2)记![]() ,设
,设![]() 是函数
是函数![]() 的两个极值点,且
的两个极值点,且![]() .
.
① 若![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
② 判断函数![]() 的零点个数,并说明理由.
的零点个数,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,且椭圆
,且椭圆![]() 的离心率为
的离心率为![]() ,过
,过![]() 作
作![]() 轴的垂线与椭圆
轴的垂线与椭圆![]() 交于
交于![]() 两点,且
两点,且![]() ,动点
,动点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)记椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,且直线
,且直线![]() 的斜率分别与直线
的斜率分别与直线![]() (
(![]() 为坐标原点)的斜率相同,动点
为坐标原点)的斜率相同,动点![]() 不与
不与![]() 重合,求
重合,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“石头、剪刀、布”,又称“猜丁壳”,是一种流行多年的猜拳游戏,起源于中国,然后传到日本、朝鲜等地,随着亚欧贸易的不断发展,它传到了欧洲,到了近代逐渐风靡世界.其游戏规则是:出拳之前双方齐喊口令,然后在语音刚落时同时出拳,握紧的拳头代表“石头”,食指和中指伸出代表“剪刀”,五指伸开代表“布”.“石头”胜“剪刀”、“剪刀”胜“布”、而“布”又胜过“石头”.若所出的拳相同,则为和局.小军和大明两位同学进行“五局三胜制”的“石头、剪刀、布”游戏比赛,则小军和大明比赛至第四局小军胜出的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,斜率为1的直线与椭圆
,斜率为1的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,其中
,其中![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设过点![]() 且与直线
且与直线![]() 平行的直线与椭圆
平行的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,若点
两点,若点![]() 满足
满足![]() ,且
,且![]() 与椭圆
与椭圆![]() 的另一个交点为
的另一个交点为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中装有9只球,其中标有数字1,2,3,4的小球各2个,标数字5的小球有1个.从袋中任取3个小球,每个小球被取出的可能性都相等,用![]() 表示取出的3个小球上的最大数字.
表示取出的3个小球上的最大数字.
(1)求取出的3个小球上的数字互不相同的概率;
(2)求随机变量![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com