
【题目】已知函数![]() .
.
(Ⅰ)若![]() 在
在![]() 存在最小值,求
存在最小值,求![]() 的取值范围;
的取值范围;
(Ⅱ)当![]() 时,证明:
时,证明: ![]() .
.
【答案】(1)![]() 在
在![]() 上无最小值.(2)见解析
上无最小值.(2)见解析
【解析】试题分析:(Ⅰ)对函数![]() 求导,分情况讨论单调性,当
求导,分情况讨论单调性,当![]() 有最小值时,求出实数
有最小值时,求出实数![]() 的范围;(Ⅱ)本题分两部分证明,先证明
的范围;(Ⅱ)本题分两部分证明,先证明![]() ,由(Ⅰ)的讨论容易得到,再证明
,由(Ⅰ)的讨论容易得到,再证明![]() ,这是构造函数
,这是构造函数![]() ,求导得出函数
,求导得出函数![]() 在
在![]() 上为增函数,所以
上为增函数,所以![]() ,就可证明
,就可证明![]() ,结合
,结合![]() 和
和![]() ,便可得出结论.
,便可得出结论.
试题解析(Ⅰ)解: 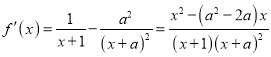
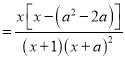 ,
,
令![]() ,解得:
,解得: ![]() 或
或![]() .
.
(1)当![]() 时,即
时,即![]() ,由
,由![]() 知,
知, ![]() ,
,
故![]() 在
在![]() 上单调递增,从而
上单调递增,从而![]() 在
在![]() 上无最小值.
上无最小值.
(2)当![]() 时,又
时,又![]() ,故
,故![]() ,
,
当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,
,
从而![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
从而![]() 在
在![]() 处取得最小值,所以
处取得最小值,所以![]() 时,
时, ![]() 存在最小值.
存在最小值.
综上所述: ![]() 在
在![]() 存在最小值时,
存在最小值时, ![]() 的取值范围为
的取值范围为![]() .
.
(Ⅱ)证明:由(Ⅰ)知, ![]() 时,
时, ![]() 在
在![]() 上单调递增;
上单调递增;
于是![]() 时,
时, ![]() ,即
,即![]() 时,
时, ![]() .①
.①
下证: ![]() ,
,
令![]() ,则
,则![]() ,故
,故![]() ,
,
由于![]() ,所以
,所以![]() ,从而
,从而![]() 在
在![]() 上单调递增,
上单调递增,
于是![]() ,从而
,从而![]() 在
在![]() 上单调递增,
上单调递增,
故![]() ,所以
,所以![]() ,②
,②
由于![]() ,所以①②可得:
,所以①②可得: ![]() ,
,
即: ![]() .
.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:
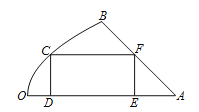
【题目】如图是一块地皮![]() ,其中
,其中![]() ,
, ![]() 是直线段,曲线段
是直线段,曲线段![]() 是抛物线的一部分,且点
是抛物线的一部分,且点![]() 是该抛物线的顶点,
是该抛物线的顶点, ![]() 所在的直线是该抛物线的对称轴.经测量,
所在的直线是该抛物线的对称轴.经测量, ![]() km,
km, ![]() km,
km, ![]() .现要从这块地皮中划一个矩形
.现要从这块地皮中划一个矩形![]() 来建造草坪,其中点
来建造草坪,其中点![]() 在曲线段
在曲线段![]() 上,点
上,点![]() ,
, ![]() 在直线段
在直线段![]() 上,点
上,点![]() 在直线段
在直线段![]() 上,设
上,设![]() km,矩形草坪
km,矩形草坪![]() 的面积为
的面积为![]() km2.
km2.
(1)求![]() ,并写出定义域;
,并写出定义域;
(2)当![]() 为多少时,矩形草坪
为多少时,矩形草坪![]() 的面积最大?
的面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图甲,已知矩形![]() 中,
中, ![]() 为
为![]() 上一点,且
上一点,且![]() ,垂足为
,垂足为![]() ,现将矩形
,现将矩形![]() 沿对角线
沿对角线![]() 折起,得到如图乙所示的三棱锥
折起,得到如图乙所示的三棱锥![]() .
.

(Ⅰ)在图乙中,若![]() ,求
,求![]() 的长度;
的长度;
(Ⅱ)当二面角![]() 等于
等于![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=1﹣ ![]() (x>0),若存在实数a,b(a<b),使y=f(x)的定义域为(a,b)时,值域为(ma,mb),则实数m的取值范围是( )
(x>0),若存在实数a,b(a<b),使y=f(x)的定义域为(a,b)时,值域为(ma,mb),则实数m的取值范围是( )
A.![]()
B.![]()
C.![]() 且m≠0
且m≠0
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】各项均为正数的数列{an}中,a1=1,Sn是数列{an}的前n项和,对任意n∈N* , 有2Sn=2pan2+pan﹣p(p∈R)
(1)求常数p的值;
(2)求数列{an}的通项公式;
(3)记bn= ![]() ,求数列{bn}的前n项和T.
,求数列{bn}的前n项和T.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前项n和为Sn , 且3Sn=4an﹣4.又数列{bn}满足bn=log2a1+log2a2+…+log2an .
(1)求数列{an}、{bn}的通项公式;
(2)若 ![]() ,求使得不等式
,求使得不等式 ![]() 恒成立的实数k的取值范围.
恒成立的实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xm﹣ ![]() ,且f(3)=
,且f(3)= ![]() .
.
(1)求函数f(x)的解析式,并判断函数f(x)的奇偶性.
(2)证明函数f(x)在(0,+∞)上的单调性.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com