
如图,在平面四边形ABCD中,AB=AD=1,∠BAD=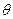 ,△BCD是正三角形。
,△BCD是正三角形。
(I)将四边形ABCD的面积S表示为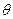 的函数;
的函数;
(II)求四边形ABCD的面积S的最大值及此时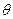 的值。
的值。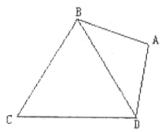
科目:高中数学 来源: 题型:解答题
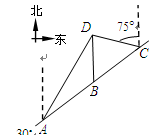
如图,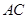 是佛山市一环东线的一段,其中
是佛山市一环东线的一段,其中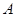 、
、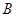 、
、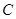 分别是林上路、佛陈路、花卉大道出口,经测量陈村花卉世界
分别是林上路、佛陈路、花卉大道出口,经测量陈村花卉世界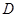 位于点
位于点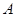 的北偏东
的北偏东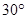 方向
方向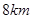 处,位于点
处,位于点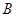 的正北方向,位于点
的正北方向,位于点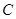 的北偏西
的北偏西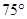 方向上,并且
方向上,并且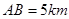 .
.
(1) 求佛陈路出口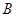 与花卉世界
与花卉世界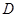 之间的距离;(精确到0.1km)
之间的距离;(精确到0.1km)
(2) 求花卉大道出口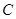 与花卉世界
与花卉世界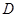 之间的距离.(精确到0.1km)
之间的距离.(精确到0.1km)
(参考数据: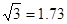 ,
,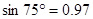 ,
,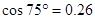 ,
,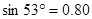 ,
,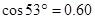 ,
, 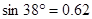 ,
,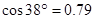
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
有一道题目由于纸张破损,有一条件看不清楚,具体如下:
(1)在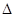 ABC中,已知
ABC中,已知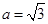 , ,
, ,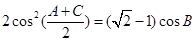 ,求角A.
,求角A.
(2)经推断,破损处的条件为三角形一边的长度,该题的答案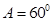 是唯一确定的,试将条件补充完整,并说明理由.
是唯一确定的,试将条件补充完整,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,已知△AOB,∠AOB=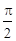 ,∠BAO=
,∠BAO=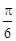 ,AB=4,D为线段AB的中点.若△AOC是△AOB绕直线AO旋转而成的.记二面角B-AO-C的大小为
,AB=4,D为线段AB的中点.若△AOC是△AOB绕直线AO旋转而成的.记二面角B-AO-C的大小为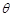 .
.
(Ⅰ)当平面COD⊥平面AOB时,求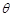 的值;
的值;
(Ⅱ)当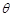 ∈[
∈[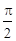 ,
,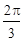 ]时,求二面角C-OD-B的余弦值的取值范围.
]时,求二面角C-OD-B的余弦值的取值范围.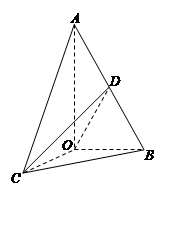
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(12分)为进行科学实验,观测小球A、B在两条相交成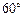 角的直线型轨道上
角的直线型轨道上
运动的情况,如图(乙)所示,运动开始前,A和B分别距O点3m和1m,后来它们同时
以每分钟4m的速度各沿轨道 按箭头的方向运动。问:
按箭头的方向运动。问:
(1)运动开始前,A、B的距离是多少米?(结果保留三位有效数字)。
(2)几分钟后,两个小球的距离最小?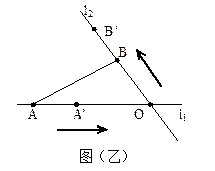
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com