分析:①画可行域②设z=3x+4y,z为目标直线的纵截距的四分之一③画直线0=3x+4y,平移直线过A或B时z有最大、小值④从而求出3x+4y-7的范围,进一步求出|3x+4y-7|的最大值.
解答: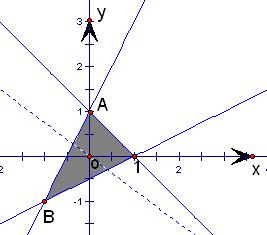
解:画可行域如图,
设z=3x+4y,z可看成是直线z=3x+4y的纵截距的四分之一,
由
⇒A(0,1),
⇒B(-1,-1).
画直线0=3x+4y,平移直线过A(0,1)点时z有最大值4;
平移直线过B(-1,-1)点时z有最小值-7;
∴-7≤3x+4y≤4
⇒-14≤3x+4y-7≤-3
⇒3≤|3x+4y-7|≤14.
则|3x+4y-7|的最大值为14
故选D.
点评:本题考查线性规划问题,难度较小.目标函数有唯一最优解是我们最常见的问题,这类问题一般要分三步:画出可行域、求出关键点、定出最优解.

 解:画可行域如图,
解:画可行域如图,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案