
【题目】某媒体为调查喜爱娱乐节目A是否与观众性别有关,随机抽取了30名男性和30名女性观众,抽查结果用等高条形图表示如图:
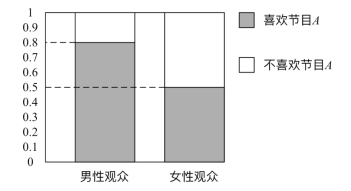
根据该等高条形图,完成下列2×2列联表,并用独立性检验的方法分析,能否在犯错误的概率不超过0.05的前提下认为喜欢娱乐节目A与观众性别有关?
喜欢节目A | 不喜欢节目A | 总计 | |
男性观众 | |||
女性观众 | |||
总计 | 60 |
附: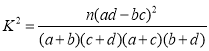
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A.经过任意三点有且只有一个平面.
B.过点![]() 有且仅有一条直线与异面直线
有且仅有一条直线与异面直线![]() 垂直.
垂直.
C.一条直线与一个平面平行,它就和这个平面内的任意一条直线平行.
D.面![]() 与平面
与平面![]() 相交,则公共点个数为有限个.
相交,则公共点个数为有限个.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《九章算术》中有云:“有木长三丈,围之八尺,葛生其下,缠木两周,上与木齐,问葛长几何?”意思为:圆木长3丈,圆周为8尺,葛藤从圆木的底部开始向上生长,绕圆木两周,刚好顶部与圆木平齐,问葛藤最少长几尺(注:1丈即10尺)?该问题的答案为34尺.若圆木长为3尺,圆周为2尺,同样绕圆木两周刚好顶部与圆木平齐,那葛藤最少又是长( )尺?
A.34尺B.5尺C.6尺D.4尺
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电信公司为了加强新用5G技术的推广使用,为该公司的用户制定了一套5G月消费返流量费的套餐服务方案;当月消费金额不超过100元时,按消费金额的![]() 进行返还;当月消费金额超过100元时,除消费金额中的100元仍按
进行返还;当月消费金额超过100元时,除消费金额中的100元仍按![]() 进行返还外,若另超出100元的部分消费金额为A元,则超过部分按
进行返还外,若另超出100元的部分消费金额为A元,则超过部分按![]() 进行返还,记用户当月返还所得流量费y(单位:元),消费金额x(单位:元)
进行返还,记用户当月返还所得流量费y(单位:元),消费金额x(单位:元)
(1)写出该公司用户月返还所得流量费的函数模型;
(2)如果用户小李当月获返还的流量费是12元,那么他这个月的消费金额是多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了释放学生压力,某校高三年级一班进行了一个投篮游戏,其间甲、乙两人轮流进行篮球定点投篮比赛(每人各投一次为一轮).在相同的条件下,每轮甲乙两人站在同一位置,甲先投,每人投一次篮,两人有1人命中,命中者得1分,未命中者得-1分;两人都命中或都未命中,两人均得0分.设甲每次投篮命中的概率为![]() ,乙每次投篮命中的概率为
,乙每次投篮命中的概率为![]() ,且各次投篮互不影响.
,且各次投篮互不影响.
(1)经过1轮投篮,记甲的得分为![]() ,求
,求![]() 的分布列及期望;
的分布列及期望;
(2)用![]() 表示经过第
表示经过第![]() 轮投篮后,甲的累计得分高于乙的累计得分的概率,求
轮投篮后,甲的累计得分高于乙的累计得分的概率,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com