
分析 根据函数与方程的关系,利用参数分离式进行转化,构造函数,求出函数的导数,研究函数的单调性和极值,利用数形结合进行求解即可.
解答 解:由ln|x|-ax2+$\frac{3}{2}$=0,得ax2=ln|x|+$\frac{3}{2}$,
∵x≠0,
∴方程等价为a=$\frac{ln|x|+\frac{3}{2}}{{x}^{2}}$,
设f(x)=$\frac{ln|x|+\frac{3}{2}}{{x}^{2}}$,
则函数f(x)是偶函数,
当x>0时,f(x)=$\frac{lnx+\frac{3}{2}}{{x}^{2}}$,
则f′(x)=$\frac{\frac{1}{x}•{x}^{2}-(lnx+\frac{3}{2})•2x}{{x}^{4}}$=$\frac{-2x(1+lnx)}{{x}^{4}}$,
由f′(x)>0得-2x(1+lnx)>0,得1+lnx<0,即lnx<-1,得0<x<$\frac{1}{e}$,此时函数单调递增,
由f′(x)<0得-2x(1+lnx)<0,得1+lnx>0,即lnx>-1,得x>$\frac{1}{e}$,此时函数单调递减,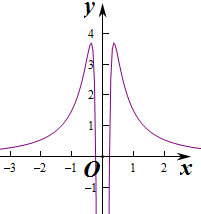
即当x>0时,x=$\frac{1}{e}$时,函数f(x)取得极大值f($\frac{1}{e}$)=$\frac{ln\frac{1}{e}+\frac{3}{2}}{(\frac{1}{e})^{2}}$
=(-1+$\frac{3}{2}$)e2=$\frac{1}{2}$e2,
作出函数f(x)的图象如图:
要使a=$\frac{ln|x|+\frac{3}{2}}{{x}^{2}}$,
有4个不同的交点,
则满足0<a<$\frac{{e}^{2}}{2}$,
故答案为:$({0,\frac{e^2}{2}})$.
点评 本题主要考查函数与方程的应用,利用参数分离法,构造函数,研究函数的单调性和极值,借助数形结合是解决本题的关键.综合性较强,有一定的难度.


 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{5}{13}$ | B. | $\frac{5}{13}$ | C. | $-\frac{12}{5}$ | D. | $\frac{12}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {an}为首项为正项的等比数列,若a2n-1+a2n<0,则公比q<0 | |
| B. | 若{an}为递增数列,则an+1>|an| | |
| C. | {an}为等差数列,若Sn+1>Sn,则{an}单调递增 | |
| D. | {an}为等差数列,若{an}单调递增,则Sn+1>Sn. |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,-1] | B. | [-2,0] | C. | [0,$\frac{6}{5}$] | D. | [-2,$\frac{6}{5}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com