Question

9．下列命题中正确命题的序号为①②③④．（写出所有正确命题的序号）
①用符号表示“点A在直线a上，直线b在平面α外，直线l与平面β相交于点B”为A∈a，b?α，l∩β=B；
②如果直线AB、CD是两条异面直线，那么直线AC、BD是异面直线；
③直线a∥平面α，直线b⊥平面α，则a⊥b；
④四面体ABCD中，若AB⊥CD，AD⊥BC，则AC⊥BD．

Answer 1

分析 在①中，由点在直线上，直线在平面外，直线与平面相交于点的表示法能判断①的正误；在②中使用反证法能判断②的正误；在③中，由直线与平面平行和直线与平面垂直的性质定理得a⊥b；在④中，要证线线垂直，可先证线面垂直，进而由线面垂直的定义（或性质）得出线线垂直．

解答 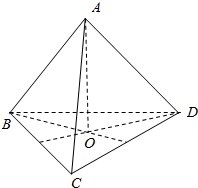解：①点A在直线a上，表示为A∈a；直线b在平面α外，表示为b?α；直线l与平面β相交于点B，表示为l∩β=B．故①正确；
②假设直线AC、BD是共面直线，则A、B、C、D共面，则直线AB、CD是两条共面直线，
这与直线AB、CD是两条异面直线相矛盾，故直线AC、BD是异面直线，故②正确；
③∵直线a∥平面α，直线b⊥平面α，∴由直线与平面平行和直线与平面垂直的性质定理得a⊥b，故③正确；
④过A作AO⊥平面BCD，垂足为O，则AO⊥CD．∵AB⊥CD，AO∩AB=A，∴CD⊥平面ABO．∵BO?平面ABO，∴CD⊥BO．
同理BC⊥DO．则O为△BCD的重心，
∴CO⊥BD．∵AO⊥BD，CO∩AO=O，
∴BD⊥平面ACO，∴AC?平面ACO，∴AC⊥BD．故④正确．
故答案为：①②③④．

点评 本题考查命题真假的判断，是中档题，解题时要认真审题，注意空间思维能力的培养．