Question

6．已知直线l：2x-y+m=0，m∈R，圆C：x²+y²=5．
（Ⅰ）当m为何值时，l与C无公共点；
（Ⅱ）当m为何值时，l被C截得的弦长为2．

Answer 1

分析 （Ⅰ）根直线和圆的位置关系进行求解即可；
（Ⅱ）根据直线和圆相交时的弦长公式进行求解即可．

解答 解：（Ⅰ）由已知，圆心为O（0，0），半径r=$\sqrt{5}$，
圆心到直线2x-y+m=0的距离d=$\frac{|m|}{{\sqrt{{2^2}+{{（-1）}^2}}}}$=$\frac{|m|}{\sqrt{5}}$，…（2分）
∵直线与圆无公共点，∴d＞r，即$\frac{|m|}{\sqrt{5}}$＞$\sqrt{5}$，…（4分）
∴m＞5或m＜-5．
故当m＞5或m＜-5时，直线与圆无公共点．…（5分）
（Ⅱ）如图，由平面几何垂径定理知r²-d²=1²．…（7分）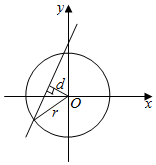

即5-$\frac{m2}{5}$=1，得m=±2$\sqrt{5}$，
∴当m=±2$\sqrt{5}$时，直线被圆截得的弦长为2．…（10分）

点评 本题主要考查直线和圆的位置关系的判断和应用，根据直线和圆相交时的弦长公式是解决本题的关键．