
已知直线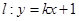 过定点
过定点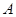 ,动点
,动点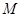 满足
满足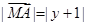 ,动点
,动点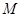 的轨迹为
的轨迹为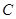 .
.
(Ⅰ)求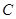 的方程;
的方程;
(Ⅱ)直线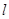 与
与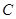 交于
交于 两点,以
两点,以 为切点分别作
为切点分别作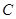 的切线,两切线交于点
的切线,两切线交于点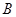 .
.
①求证: ;②若直线
;②若直线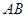 与
与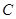 交于
交于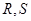 两点,求四边形
两点,求四边形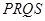 面积的最大值.
面积的最大值.
(1)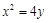 (2) 根据直线斜率互为负倒数来得到证明,当且仅当
(2) 根据直线斜率互为负倒数来得到证明,当且仅当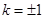 时,四边形
时,四边形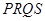 面积的取到最小值
面积的取到最小值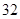 。
。
【解析】
试题分析:(I)由题意知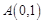 ,设
,设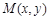
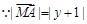
 化简得
化简得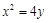 3分
3分
(Ⅱ)①设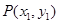 ,
,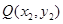 ,
,
由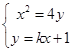 消去
消去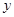 ,得
,得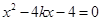 ,显然
,显然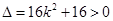 .
.
所以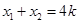 ,
,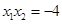
由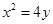 ,得
,得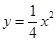 ,所以
,所以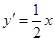 ,
,
所以,以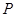 为切点的切线的斜率为
为切点的切线的斜率为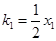 ,
,
所以,以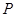 为切点的切线方程为
为切点的切线方程为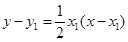 ,又
,又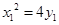 ,
,
所以,以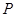 为切点的切线方程为
为切点的切线方程为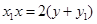 ……(1)
……(1)
同理,以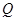 为切点的切线方程为
为切点的切线方程为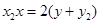 ……(2)
……(2)
(2)-(1)并据 得点
得点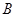 的横坐标
的横坐标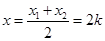 ,
,
代入(1)易得点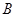 的纵坐标
的纵坐标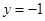 ,所以点
,所以点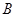 的坐标为
的坐标为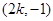
当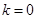 时,显然
时,显然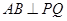
当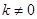 时,
时,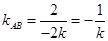 ,从而
,从而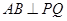 8分
8分
②由已知,显然直线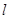 的斜率不为0,由①知
的斜率不为0,由①知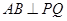 ,所以
,所以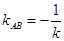 ,
,
则直线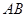 的方程为
的方程为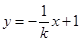 ,
,
设设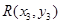 ,
,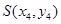 ,
,
由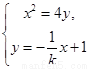 消去
消去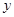 ,得
,得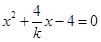 ,显然
,显然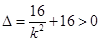 ,
,
所以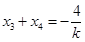 ,
,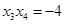 .
.
又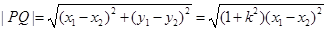
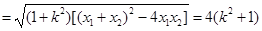
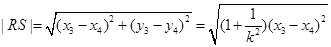
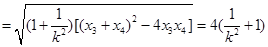
因为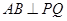 ,所以
,所以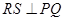 ,
,
所以,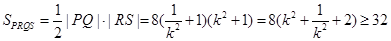 ,
,
当且仅当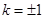 时,四边形
时,四边形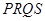 面积的取到最小值
面积的取到最小值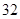 13分
13分
考点:直线与抛物线的位置关系
点评:解决的关键是借助于向量的模来表示得到轨迹方程,并联立方程组来得到弦长公式,进而得到面积的表示,属于中档题。


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| PQ |
| RS |
| AB |
| AF |
| TB |
| FT |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知直角坐标平面内的动点M满足:|MA|2-|MB|2=4(|MB|-1),其中A(0,-1),B(0,1).
已知直角坐标平面内的动点M满足:|MA|2-|MB|2=4(|MB|-1),其中A(0,-1),B(0,1).查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分14分)
平面直角坐标系中,已知直线![]() :
:![]() ,定点
,定点![]() ,动点
,动点![]() 到直线
到直线![]() 的距离是到定点
的距离是到定点![]() 的距离的2倍.
的距离的2倍.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)若![]() 为轨迹
为轨迹![]() 上的点,以
上的点,以![]() 为圆心,
为圆心,![]() 长为半径作圆
长为半径作圆![]() ,若过点
,若过点![]() 可作圆
可作圆![]() 的两条切线
的两条切线![]() ,
,![]() (
(![]() ,
,![]() 为切点),求四边形
为切点),求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com