
分析 作AA1⊥x轴,BB1⊥x轴.则可知AA1∥OF∥BB1,根据比例线段的性质可知$\frac{|FB|}{|AF|}$=$\frac{|O{B}_{1}|}{|O{A}_{1}|}$=$\frac{|{x}_{B}|}{|{x}_{A}|}$,根据抛物线的焦点和直线的倾斜角可表示出直线的方程,与抛物线方程联立消去x,根据韦达定理求得xA+xB和xAxB的表达式,进而可求得xAxB=-($\frac{{x}_{A}+{x}_{B}}{\frac{2\sqrt{3}}{3}}$)2,整理后两边同除以xA2得关于$\frac{{x}_{B}}{{x}_{A}}$的一元二次方程,求得$\frac{{x}_{B}}{{x}_{A}}$的值,进而求得$\frac{|FB|}{|AF|}$.
解答 解:如图,作AA1⊥x轴,BB1⊥x轴.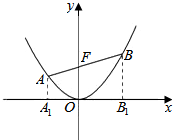
则AA1∥OF∥BB1,
∴$\frac{|FB|}{|AF|}$=$\frac{|O{B}_{1}|}{|O{A}_{1}|}$=$\frac{|{x}_{B}|}{|{x}_{A}|}$,
又已知xA<0,xB>0,
∴$\frac{|FB|}{|AF|}$=-$\frac{{x}_{B}}{{x}_{A}}$,
∵直线AB方程为y=xtan30°+$\frac{p}{2}$
即y=$\frac{\sqrt{3}}{3}$x+$\frac{p}{2}$,
与x2=2py联立得x2-$\frac{2\sqrt{3}}{3}$px-p2=0
∴xA+xB=$\frac{2\sqrt{3}}{3}$p,xA•xB=-p2,
∴xAxB=-p2=-($\frac{{x}_{A}+{x}_{B}}{\frac{2\sqrt{3}}{3}}$)2
=-$\frac{3}{4}$(xA2+xB2+2xAxB)
∴3xA2+3xB2+10xAxB=0
两边同除以xA2(xA2≠0)得
3($\frac{{x}_{B}}{{x}_{A}}$)2+10$\frac{{x}_{B}}{{x}_{A}}$+3=0
∴$\frac{{x}_{B}}{{x}_{A}}$=-3或-$\frac{1}{3}$.
又∵xA+xB=$\frac{2\sqrt{3}}{3}$p>0,
∴xA>-xB,
∴$\frac{{x}_{B}}{{x}_{A}}$<-1,
∴$\frac{|FB|}{|AF|}$=-$\frac{{x}_{B}}{{x}_{A}}$=3.
故答案为:3
点评 本题主要考查了抛物线的性质,直线与抛物线的关系以及比例线段的知识.考查了学生综合分析问题和解决问题的能力.


科目:高中数学 来源: 题型:选择题
| A. | {0,1} | B. | {-1,1} | C. | {1} | D. | {-1,0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 1 | 2 | 3 | 4 | 5 |
| y | 2.9 | 3.3 | 3.6 | 4.4 | 5.1 |
| u | 1 | 2 | 3 | 4 | 5 |
| v | 25 | 20 | 21 | 15 | 13 |
| A. | 变量x与y正相关,u与v正相关 | B. | 变量x与y负相关,u与v正相关 | ||
| C. | 变量x与y负相关,u与v负相关 | D. | 变量x与y正相关,u与v负相关 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜好体育运动 | 不喜好体育运动 | 合计 | |
| 男生 | 5 | ||
| 女生 | 10 | ||
| 合计 | 50 |
| P(k2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{3}$个单位 | B. | 向右平移$\frac{π}{3}$个单位 | ||
| C. | 向左平移$\frac{π}{6}$个单位 | D. | 向右平移$\frac{2π}{3}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
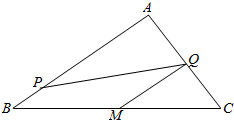 如图,在Rt△ABC中,AB=4,AC=3,∠A=90°,$\overrightarrow{AP}$=m$\overrightarrow{PB}$,$\overrightarrow{AQ}$=n$\overrightarrow{QC}$,m,n>0,且满足$\frac{1}{m}$+$\frac{1}{n}$=$\frac{1}{2}$,M是BC的中点,对任意的λ∈R,|λ•$\overrightarrow{QP}$+$\overrightarrow{QM}$|的最小值记为f(m),则对任意m>0,f(m)的最大值为$\frac{1}{2}$.
如图,在Rt△ABC中,AB=4,AC=3,∠A=90°,$\overrightarrow{AP}$=m$\overrightarrow{PB}$,$\overrightarrow{AQ}$=n$\overrightarrow{QC}$,m,n>0,且满足$\frac{1}{m}$+$\frac{1}{n}$=$\frac{1}{2}$,M是BC的中点,对任意的λ∈R,|λ•$\overrightarrow{QP}$+$\overrightarrow{QM}$|的最小值记为f(m),则对任意m>0,f(m)的最大值为$\frac{1}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com