
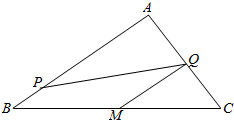
 如图,在Rt△ABC中,AB=4,AC=3,∠A=90°,$\overrightarrow{AP}$=m$\overrightarrow{PB}$,$\overrightarrow{AQ}$=n$\overrightarrow{QC}$,m,n>0,且满足$\frac{1}{m}$+$\frac{1}{n}$=$\frac{1}{2}$,M是BC的中点,对任意的λ∈R,|λ•$\overrightarrow{QP}$+$\overrightarrow{QM}$|的最小值记为f(m),则对任意m>0,f(m)的最大值为$\frac{1}{2}$.
如图,在Rt△ABC中,AB=4,AC=3,∠A=90°,$\overrightarrow{AP}$=m$\overrightarrow{PB}$,$\overrightarrow{AQ}$=n$\overrightarrow{QC}$,m,n>0,且满足$\frac{1}{m}$+$\frac{1}{n}$=$\frac{1}{2}$,M是BC的中点,对任意的λ∈R,|λ•$\overrightarrow{QP}$+$\overrightarrow{QM}$|的最小值记为f(m),则对任意m>0,f(m)的最大值为$\frac{1}{2}$. 分析 建立如图所示的坐标系,可得A、B、CM的坐标,求得P、Q的坐标,由|λ•$\overrightarrow{QP}$+$\overrightarrow{QM}$|的最小值等于点M到直线PQ的距离,求得f(m)的解析式,再根据它的几何意义求得它的范围,可得它的最大值.
解答 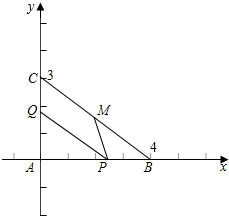 解:建立如图所示的坐标系,则A(0,0),B(4,0),C(0,3);
解:建立如图所示的坐标系,则A(0,0),B(4,0),C(0,3);
∵$\overrightarrow{AP}$=m$\overrightarrow{PB}$,$\overrightarrow{AQ}$=n$\overrightarrow{QC}$,m,n>0,有P($\frac{4m}{m+1}$,0),Q(0,$\frac{3n}{n+1}$);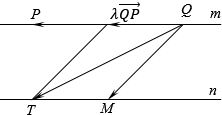
如图,λ$\overrightarrow{QP}$在直线m上,由平行四边形法则,向量λ$\overrightarrow{QP}$+$\overrightarrow{QM}$的起点为Q,终点为直线n上一点T,有$\overrightarrow{QT}$=λ$\overrightarrow{QP}$+$\overrightarrow{QM}$;
当$\overrightarrow{QT}$⊥直线n时,|λ•$\overrightarrow{QP}$+$\overrightarrow{QM}$|最小,即|λ•$\overrightarrow{QP}$+$\overrightarrow{QM}$|最小值为直线m与直线n的距离.
直线PQ:$\frac{x}{\frac{4m}{m+1}}+\frac{y}{\frac{3n}{n+1}}=1$,点M(2,$\frac{3}{2}$),
则M到PQ的距离d=$\frac{|\frac{2}{\frac{4m}{m+1}}+\frac{\frac{3}{2}}{\frac{3n}{n+1}}-1|}{\sqrt{(\frac{m+1}{4m})^{2}+(\frac{n+1}{3n})^{2}}}$=$\frac{|\frac{1}{2m}+\frac{1}{2n}|}{\sqrt{(\frac{1}{4}+\frac{1}{4}•\frac{1}{m})^{2}+(\frac{1}{3}+\frac{1}{3}•\frac{1}{n})^{2}}}$;
∵$\frac{1}{m}$+$\frac{1}{n}$=$\frac{1}{2}$,
d=$\frac{\frac{1}{4}}{\sqrt{(\frac{1}{4}+\frac{1}{4}•\frac{1}{m})^{2}+(\frac{1}{3}+\frac{1}{3}•\frac{1}{n})^{2}}}$=$\frac{1}{4\sqrt{\frac{25}{144}•(\frac{1}{m})^{2}-\frac{5}{24}•\frac{1}{m}+\frac{5}{16}}}$=f(m);
对y=$\frac{25}{144}•(\frac{1}{m})^{2}-\frac{5}{24}•\frac{1}{m}+\frac{5}{16}$为二次函数,当$\frac{1}{m}$=$\frac{3}{5}$时,y最小为$\frac{1}{4}$,
所以f(m)max=$\frac{1}{4\sqrt{\frac{1}{4}}}$=$\frac{1}{2}$.
点评 本题主要考查两个向量坐标形式的运算,向量运算的几何意义,点到直线的距离公式、函数的单调性的应用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com